みなさんこんにちは。テクノシェルパ技術コンサルタントの森です。
このブログでは、電気回路に不可欠な部品の一つであるコンデンサ（コンデンサとは電荷を蓄えたり放出したりする素子です）の原理についてご紹介します。
（当社の技術者教育サービスご紹介のページはこちら）
（電子回路の基礎講座PLUS(2日間コース)はこちら）
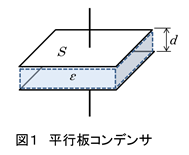図１は最も簡単なコンデンサです（平行板コンデンサといいます）。二枚の金属板は、容量Cを持ち、平行板の面積Sと距離dから以下の式として求めることができます。
C=εS/d (1)
ここで、εは平行板間を絶縁する絶縁体の誘電率です。
式(1)は容量Cが以下の関係にあることを表しています。
- 平行板の面積Sが大きければ大きいほど容量Cは大きい。
- 平行板の距離dが小さければ小さいほど容量Cは大きい。
- 平行板の間の誘電体(絶縁体）の誘電率εが大きいほど容量Cは大きい。
1.は電荷をためるのが金属板なので、面積Sに容量Cが比例するというのはイメージしやすいと思います。
2.は金属板の距離dに反比例して容量Cが大きくなるのですが、「なんで？」と思われる方が多いのではないかと思います。
これは、プラスとマイナスの電荷には引き合う力が作用するためです（この力のことを静電気力とかクーロン力と呼びます）。
下敷きで髪の毛をこすって離すと髪の毛が下敷きに引っ張られて立ったのを思い出してもらえば良いと思います。
距離dが近いほど静電気力は強く作用するので、単位面積あたりに蓄えられる電荷量が増えることになり、容量Cは増えます。
3.は平行板の間の誘電体(絶縁体）の誘電率εに比例して容量Cが大きくなるのですが、εは、真空の誘電率εoと、その物質のε0に対する比をあらわす比誘電率εrを用いて以下の式であらわされます。
ε＝ε0εｒ (2)
ここでε0 ≒ 8.85×10-12 [F/m]
よって式(1)は、
C=ε0εrS/d (3)
最も小さい誘電率は真空の誘電率ε0です（空気の誘電率もほぼ真空と同じです）。つまり、どのような誘電体もε＞ε0（εr＞１）となるのです。
このことから、真空もしくは空気を挟んだ平行板コンデンサの間になんらかの絶縁体を挿入すると容量Cは増加する、ということを知っておいてください。
さてここで、図1について容量Cが1μFの平行板コンデンサがあるとします。以下のケースについて面積Sや距離dを求めてみましょう。（ε0 ≒ 8.85×10-12 [F/m]とする）
Q1．平行板の間が空気（εr=1）で、d＝1 mmのときのSは
Q2．平行板の間が誘電体（εr＝5000）で、S=1 m2のときのdは？
Q3．平行板の間が誘電体（εr＝5000）で、d=10 μmのときのSは？
Q1を求めると、
S=dC/(εoεr)＝(1×10-3)(1×10-6)／(8.85×10-12×1) ≒113 [m2]
なんと、10 m四方の電極面積が必要になります。
次にQ2も求めてみましょう。
d=εoεrS/C＝(8.85×10-12×5000×1)／(1×10-6) ≒0.0443 [m]
面積1 m四方の電極面積と比誘電率5000の誘電体で1 μFの容量を実現するためのdは4.4 cm必要です。
最後にQ3を求めてみましょう。
S=dC/(εoεr)＝(10×10-6)(1×10-6)／(8.85×10-12×5000) ≒0.226×10-3[m2]
上記計算値のルートをとると約15 mm四方の面積があれば1 μFの容量を実現できることがわかります。Q1のときより圧倒的に小さな面積になりましたね。しかし、それでも15 mm四方のコンデンサになるんですね。
私達が使う代表的なコンデンサのセラミックコンデンサや電解コンデンサはこのように大きくはありませんね。
さて、どのような工夫をして小さなサイズのコンデンサを実現しているのでしょうか？次回のブログでは、このことについてコンデンサの種類別の構造や材料について検証し、そこからおおまかな特性や用途についてみなさんと一緒に考えてみたいと思います。
お楽しみに！
技術者教育サービスのご紹介