みなさんこんにちは。テクノシェルパ技術コンサルタントの森です。
回路公式依存の落とし穴にはまらないためのちょっとしたコツについて、
前回のブログに続きご紹介いたします。それでは早速本題に入りますね。
前回のブログでは、図3のような抵抗5本の並列回路の合成抵抗
R P2を、抵抗並列回路の公式を用いて式(3)から式(4)を導出し、この式(4)に
R 1=330 Ω，
R 2=470 Ω，
R 3=15 kΩ，
R 4=56 Ω，
R 5=100 kΩを代入して
R P2＝42.2 Ωを求めてもらいました。
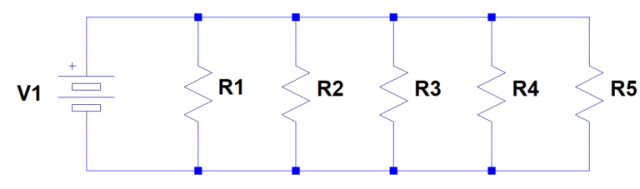
図3 抵抗並列回路(2)
しかし、公式を使って合成抵抗を求めたものの、式(4)の導出や数値の代入で間違えたり間違えそうになったりで、面倒くさく嫌気がさした方は多かったと思います。これこそが回路公式の落とし穴にはまった状態なんです。
実は、並列抵抗回路の合成抵抗は、抵抗並列回路の公式を使わなくても求めることができるんです。
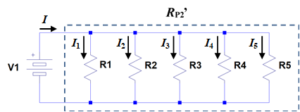
図4 抵抗並列回路(3)
図4をごらんください。図4は、図3の回路に流れる電流を追加したものです。
R 1から
R 5には各々
I 1から
I 5の電流が流れ、全回路電流
I は式(5)であらわされます。
そうです。式(5)は、キルヒホッフの第一法則なんですね。
ここで、点線で囲った回路を一つの抵抗
R P2’とみなします。
R P2’には、
V 1の電圧が印加され電流
I が流れているので、オームの法則から
で求められます。
ここで
V 1=10 Vとして前回の回路定数
R 1=330 Ω，
R 2=470 Ω，
R 3=15 kΩ，
R 4=56 Ω，
R 5=100 kΩを用いて、
I 1から
I 5を電卓を使って求めてみましょう。（
V 1は10 Vにこだわりません。みなさんが計算しやすい値で構いません）
よって全回路電流Iは、
したがって
R P2’は、
として求まります。
このように、『回路の全電流を求めることさえできたら、難しい計算式を立てなくても合成抵抗は求めることができる』んです。
回路の実務において大切なことは、まず正確にそして速く計算できることです。途中の計算過程が正しくても最後の計算をミスしてしまうと、全然違う回路定数になってしまい致命的な問題になってしまいますし、これを求めるために長々とやり直しをしながら計算していたのでは貴重な時間がいくらあっても足りません。
この回路計算の事例は、これまで私の講座を受講していただいたみなさんの内、なんと８～９割の方が抵抗並列回路の公式を用いて式(4)の導出に取り組み、そして、時間をかけても式(4)に辿り着けなかったり苦労して求めた式(4)は正しいのに最後の計算でミスをしたりと、見事に落とし穴にはまってしまう方が多数おられることから、是非みなさんに知っておいていただきたいと思い、掲載させていただきました。（このブログを読まれたみなさんはもう大丈夫ですよね。）
次のブログでもみなさんのお役立ち情報をご紹介させていただきます。お楽しみに！
＜ここがポイント！＞
抵抗並列回路の公式は、実は全回路電流から導き出されでいるので、今回ご紹介した内容はあたりまえの結果なのです。分かれ目は、式の導出の途中過程をきちんと理解しているか、あるいは根本原理に基づき回路を眺めることができるかどうかです。これらができていれば公式に依存せず効率的なアプローチで解にたどり着くことができます。
今回は一つの例として抵抗並列回路についてご紹介いたしましたが、回路の世界はいろいろな公式を駆使して回路を設計し動作を予測します。その公式はどうやって導きだされたのかを理解すると共に、別の見方でも回路動作や公式を理解することができると、その回路についての理解はさらに深まり、回路を学ぶ楽しみはいっそう増すことでしょう。
みなさんこんにちは。テクノシェルパ技術コンサルタントの森です。
回路公式依存の落とし穴にはまらないためのちょっとしたコツについて、前回のブログに続きご紹介いたします。それでは早速本題に入りますね。
前回のブログでは、図3のような抵抗5本の並列回路の合成抵抗R P2を、抵抗並列回路の公式を用いて式(3)から式(4)を導出し、この式(4)にR 1=330 Ω，R 2=470 Ω，R 3=15 kΩ，R 4=56 Ω，R 5=100 kΩを代入してR P2＝42.2 Ωを求めてもらいました。
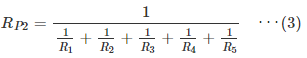
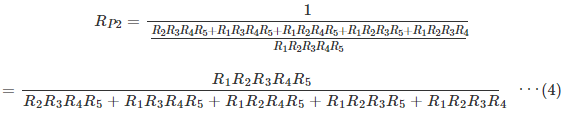
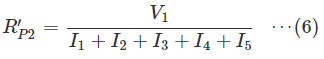
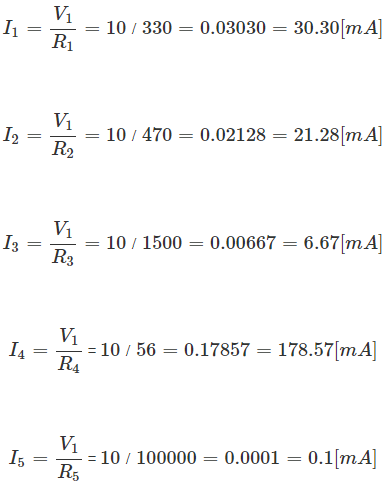
＜ここがポイント！＞
抵抗並列回路の公式は、実は全回路電流から導き出されでいるので、今回ご紹介した内容はあたりまえの結果なのです。分かれ目は、式の導出の途中過程をきちんと理解しているか、あるいは根本原理に基づき回路を眺めることができるかどうかです。これらができていれば公式に依存せず効率的なアプローチで解にたどり着くことができます。
今回は一つの例として抵抗並列回路についてご紹介いたしましたが、回路の世界はいろいろな公式を駆使して回路を設計し動作を予測します。その公式はどうやって導きだされたのかを理解すると共に、別の見方でも回路動作や公式を理解することができると、その回路についての理解はさらに深まり、回路を学ぶ楽しみはいっそう増すことでしょう。