スミスチャートを初めて見たとき、なんてヘンテコな模様なのだろうって思いませんでしたか。「円の中に模様のような曲線がいっぱい入っていて、なんだか複雑そうだし、どうしてこんな形なのだろう？」なんて思いませんでしたか。
今回は、スミスチャートの図柄を数式で表現すること抜きに、視覚的にざっくりと理解してみようという試みです。
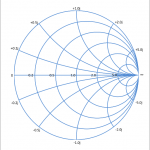
スミスチャート上にプロットするインピーダンスは複素数ですから、縦軸を虚数、横軸を実数とするＸＹグラフにプロットすることができます。
図１．XY（虚数・実数）グラフ
XY座標を使えば、図１のように、Z=R+jX という任意のインピーダンスをプロットすることは、容易にできますね。
しかし、分布定数回路の設計作業においては、XY座標は実は非常に使い勝手が悪いのです。
分布定数線回路では、無限大インピーダンスを表現する必要が出て来ることがあります。勿論、実際に無限大ということはなく、事実上、無限大と見なして差し支えないほど大きいインピーダンスということです。
そして、この無限大の扱いがXY座標では難しいのです。X座標とY座標をどこまで長く伸ばせば無限をプロットしたことになると言えるのか、ということになるからです。
この問題を解決したのがスミスチャートなんです。
スミスチャートをざっくり理解するために、少々乱暴な説明とはなりますが、とにかくえいやっと視覚的に理解してみましょう。
まず、先ほどのXY座標のうち、左半分は実抵抗のRがマイナスの値となることから、不要となり、削除します。
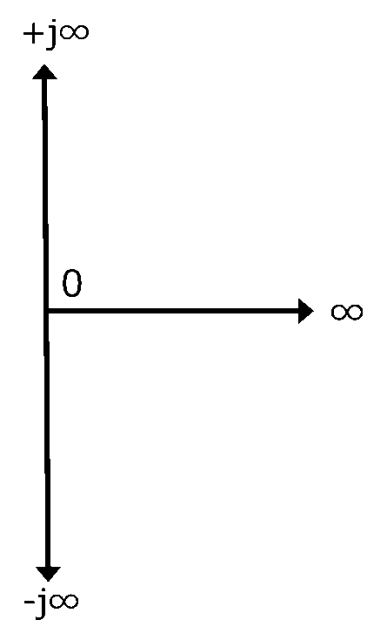
図2．XY座標からX軸(実数軸)のマイナス側を取り去ったもの
次に、虚数軸であるY軸を曲げて、軸の２つの先っぽ（「+j∞」と「-j∞」）を実軸であるX軸の右方向に近づけていきます。
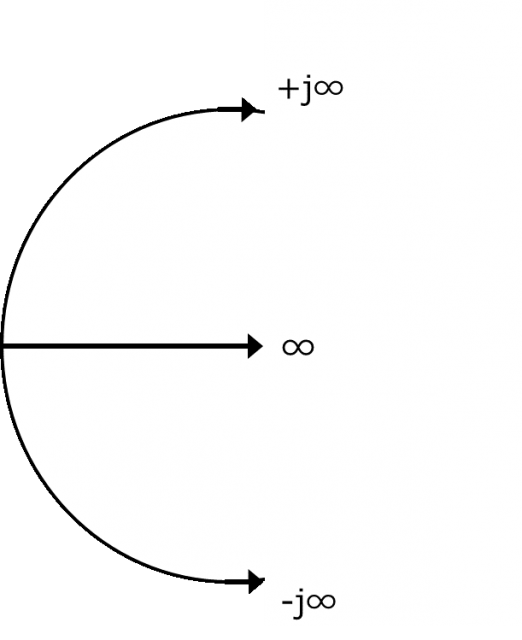
図３．Y軸(虚数軸)を右方向に曲げいく
そして、R＝∞の点とくっつけてしまいます。無限をプロットする際に厄介な無限点を１か所にまとめてしまったということです。
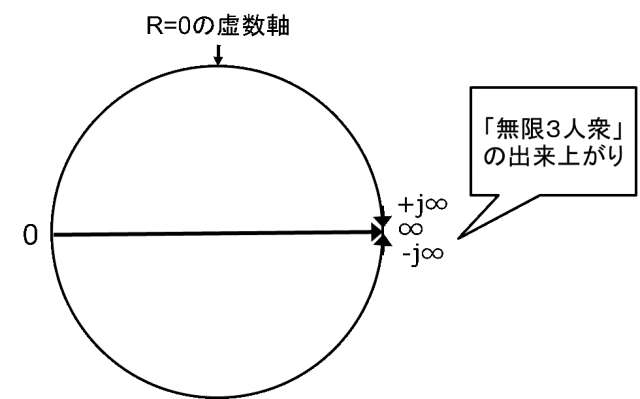
図４．+j∞、-j∞、Ｒ＝∞をくっつける
これでスミスチャートの大枠のできあがりです。
次に、スミスチャートの中の、あのごちゃごちゃしたたくさんの線に移ります。
簡単なことです。虚数軸、実軸の補助線も一緒に曲げたらあのような模様が出来上がりますよ。
虚数軸を例に取って描いてみましょう。
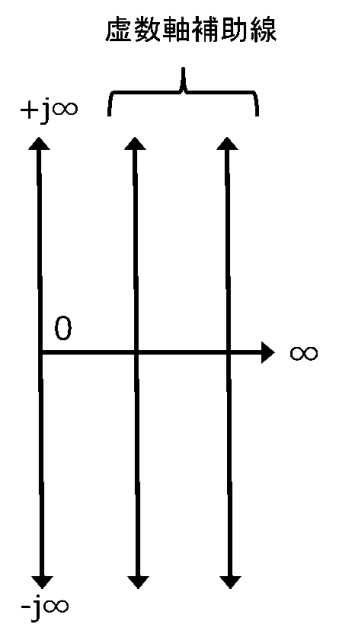
図５．図２に虚数軸補助線を追加したもの
図5のような虚数軸の補助線を伴ったグラフをまた右に曲げていきます（図６）。
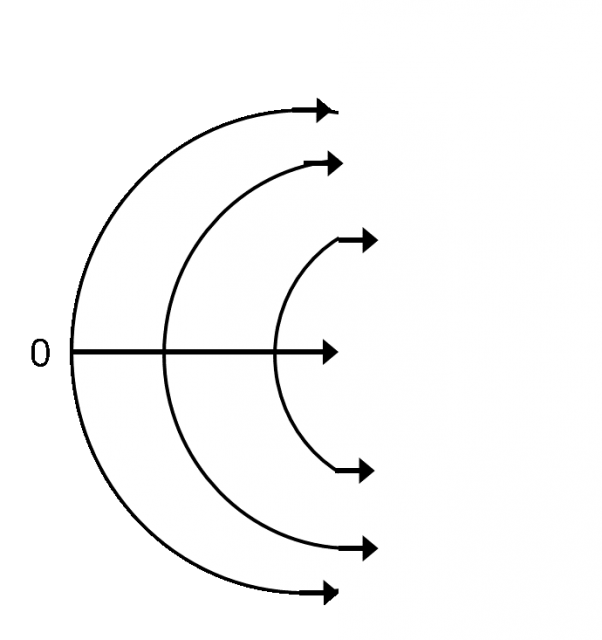
図６．Y軸(虚数軸)を補助線と共に右方向に曲げいく
そうすると、図７のようになります。
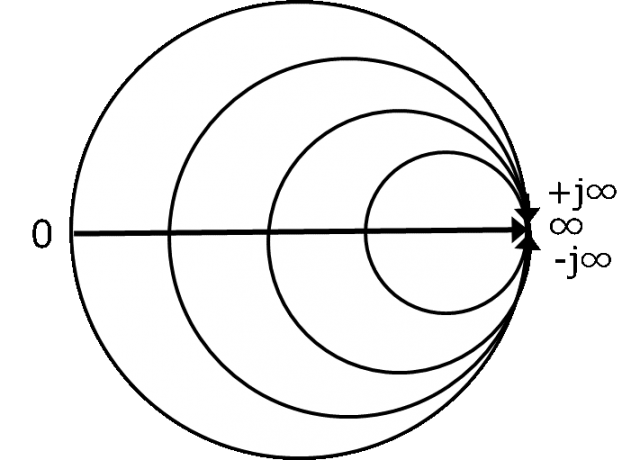
図７．虚軸補助線まで含めて変形した図
実軸の方の説明は省略しますが、同じようにやれば、図８のようなスミスチャートの模様になることは簡単に理解できると思います。
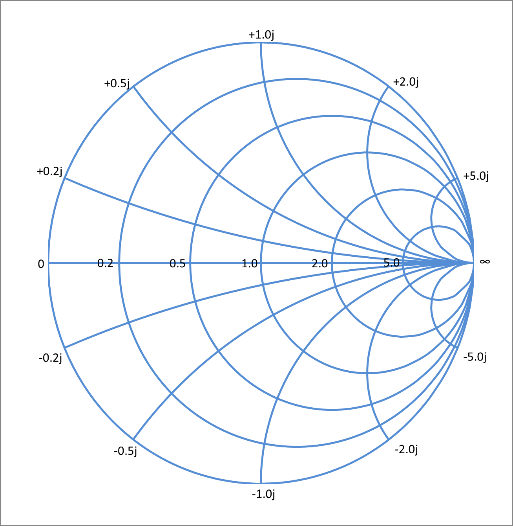
図８．スミスチャート完成図
なお、スミスチャートにインピーダンスをプロットするときは、特性インピーダンスZ0で規格化(割算)します。そのため、スミスチャート上は、単位を持たない無次元空間となります。
その結果として、同じく無次元指数である反射率も同チャート内で扱えるようになるという訳です。
なお、スミスチャートをよく見るとお気づきになると思いますが、スミスチャート内の虚数軸と実軸が交差する箇所はどこをとっても直角になっています。
これは非常に大事なことなのですが、インピーダンスの虚部と実部はそれぞれが独立変数であることから、代数学で言う「直交」変数であり、それをグラフ上でもきちんと再現しているのです。
そのために、一方の動きがもう一方に作用することが全くなく、独立を保つことができ、２次元計算尺として使えるのです。
いかがでしたでしょうか？
今回は、数学的な厳密さはさておき、感覚的にスミスチャートがどのようなものか捉えてみましょうというご提案でした。
【スミスチャート説明動画】
【関連リンク】
■技術者教育ブログ
- SSPA（Solid State Power Amplifier）の設計は機能ごとに分けて考えよう
- 分布定数回路とは？
- 同軸ケーブルの特性インピーダンスは任意に設定できるのか？
- ブログ・スミスチャートとは？ ～きちんと知ると便利です～
- ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その２）
- ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その３）
- ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その４）
- 高周波回路の基礎講座をオンデマンドで始めます！ ～Mr.Smithで学ぶインピーダンスマッチングの基礎～
■技術コンサルサービス
■高周波・無線関連ページ