
今回は2端子対回路の中にキャパシタCを並列接続したときの反射損失と通過損失を求めます。
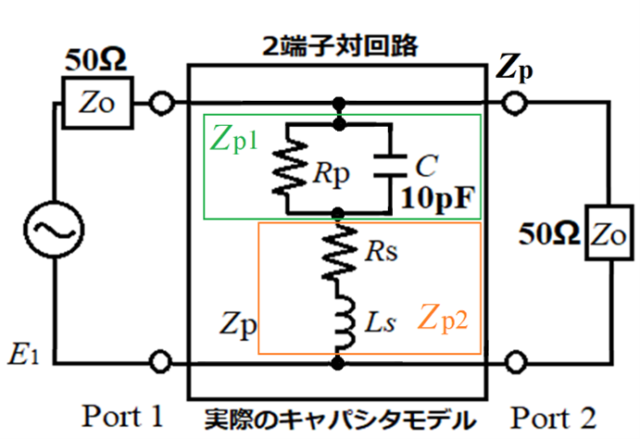
現実的なキャパシタモデルを並列に接続すると、上の回路図のようになる。
最初にZpを求めなければならないので、なみりんよZpを求めてくれないか。


Zpは、Rp、Cの2素子から成る並列インピーダンスとRs、Lsの直列インピーダンスの和で表現することができます。上の回路だと、Zp = Zp1 + Zp2で求まります。
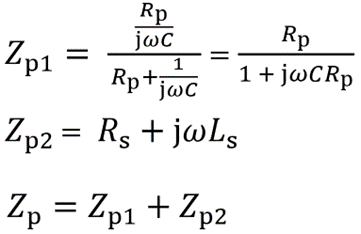
下の式を参考に、複素関数を使ってS11とS21を求めたあとに、反射損失と通過損失を求めるのじゃ。



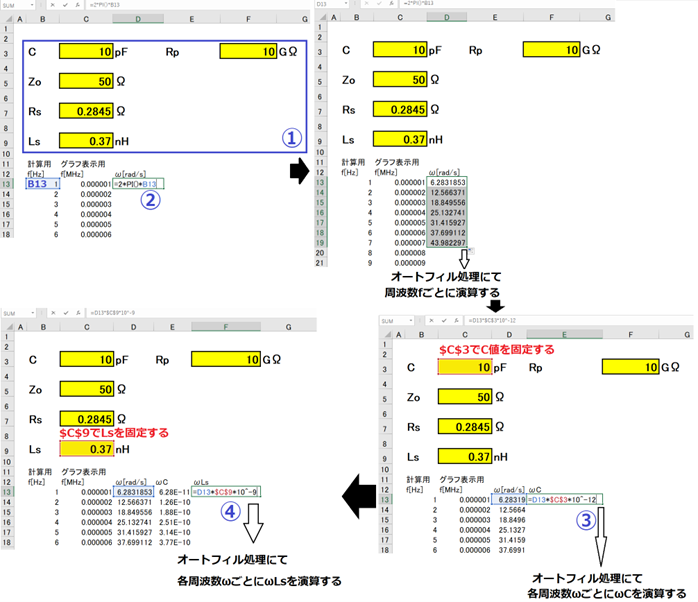
① 最初に初期条件設定として、インダクタLと各パラメータを記述します。
ここではC=10pF、Rp = 10GΩ、Rs=0.2845Ω、Ls=0.37nH、Zo=50Ωにします。
② つぎに周波数fを記述し、角速度ω( =2 π f )[rad/s]を求めます。
③ さらに角速度ωとキャパシタCとの積でωCを求めます。
④ そのうえに角速度ωと直列等価インダクタンスLsとの積でωLsを求めます。
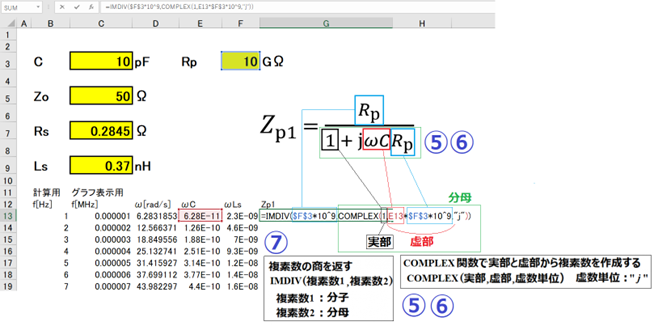
つぎはS11を求めるために複素関数を使ってまずはZpを求めてみるのじゃ。


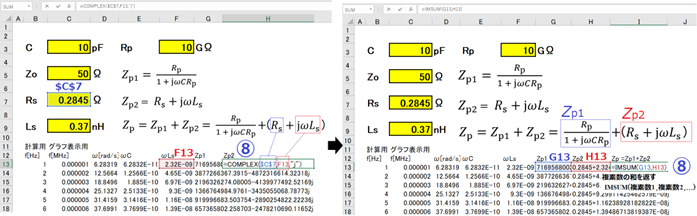
⑤ Zp = Zp1 + Zp2のうち、Zp1の分母をCOMPLEX関数で記述します。
⑥ Zp1 の分母の実数は1、虚数はωCRpになります。
⑦ Zp1 の分母を複素数化できたので、IMDIVで分子を分母で割ります。これが、Zp1です。

⑧ Zp = Zp1 + Zp2 = Zp1 +( Rs + jωLs )からZpを求めます。
Zp2 = Rs + jωLs を先に求めておきます。
つぎにZp = Zp1 + Zp2を計算します。

⑨ S11を求めます。
⑩ |S11|、反射損失を求めます。

つぎはS21を求めてみるのじゃ。


⑪ S21はZpが既知なので、すぐに求めることができます。
⑫ |S21|、通過損失を求めます。
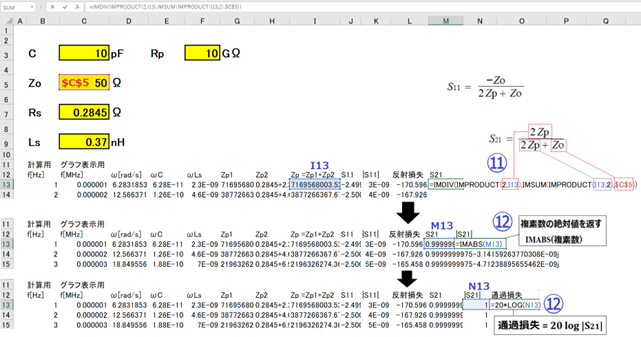
S21から通過損失も求まったようじゃな。
横軸を周波数[MHz]にして、反射損失と通過損失をグラフ化してみるのじゃ。



下のようなグラフになりました。
低周波域では通過損失が小さく、2.6GHzでは最大となり、10GHz付近では再び通過損失が小さくなるようです。
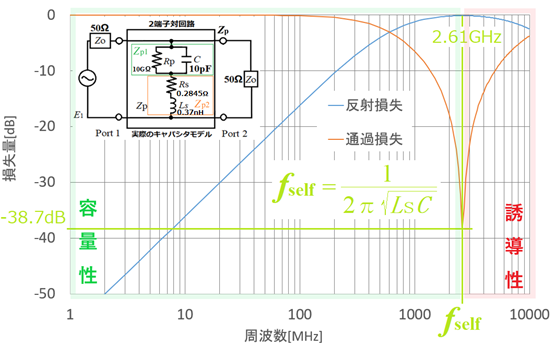
そうじゃな。
実際のキャパシタモデルを2端子対回路の中に並列で接続すると、キャパシタCと等価直列インダクタンスLsとの直列共振が形成される。そのためある周波数(自己共振周波数:fself)ではキャパシタC側に信号が全量流れこみ、Port2の出力インピーダンスZOには信号が流れなくなるのじゃ。いわゆるこの状態が全反射とよばれるものじゃ。

今回で直列素子と並列素子のSパラメータについて説明した。これで2端子対回路におけるインダクタとキャパシタを使用した周波数特性を示すことができたな。
なみりんよ、注意してほしいことがある。これまでに使用した回路モデルはすべて入力インピーダンスと出力インピーダンスが50Ωであることが前提なのじゃ。実際の伝送回路の入出力インピーダンスは50Ωではない(複素インピーダンスである)ことがほとんどである。入出力インピーダンスの実抵抗値やリアクタンス成分の影響があるので、実際に効果(または弊害)確認しなければならないぞ。


はい、実際に回路を組んだ時に周波数特性を確認してみます。
インダクタLとキャパシタCの直列接続と並列接続の動作について、エクセルの複素関数を使うことで煩雑な代数計算をすることなく簡単に周波数特性を表現することができました。
昇平博士、長い間ありがとうございました。
