
今回は2端子対回路の中にキャパシタCを実際の等価素子に置き換えたときの反射損失と通過損失を求めます。
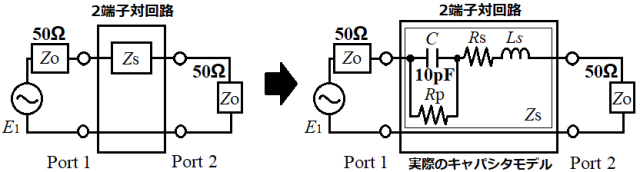
今回は2端子対回路の中にキャパシタCの代わりに実際の等価素子を代入したときのS11とS21を求めることにする。求め方は実際の等価素子の合成インピーダンスZsを求めた後に、S11とS21を解いていくとよい。各々の等価素子は、以下のように表現することができる。
C:キャパシタの公称値、Rp:等価並列抵抗、Rs:等価直列抵抗、Ls:等価直列インダクタンス


昇平博士、下の図のように今回はCとRpは、並列合成インピーダンスZs1、RsとLsは直列合成インピーダンスZs2になります。つまりZsは、Zs1とZs2の和になります。
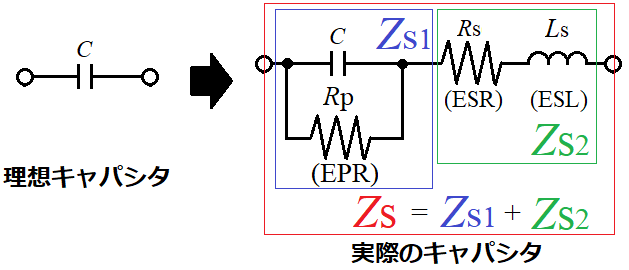
そうじゃな。Zsは多項式で表現すると複雑化し扱いがやっかいになるが、複素関数を活用してZs1、Zs2、Zsの順に1つ1つ丁寧に計算すれば、確実にS11とS21を求めることができるぞ。
ではさっそく演習じゃ。


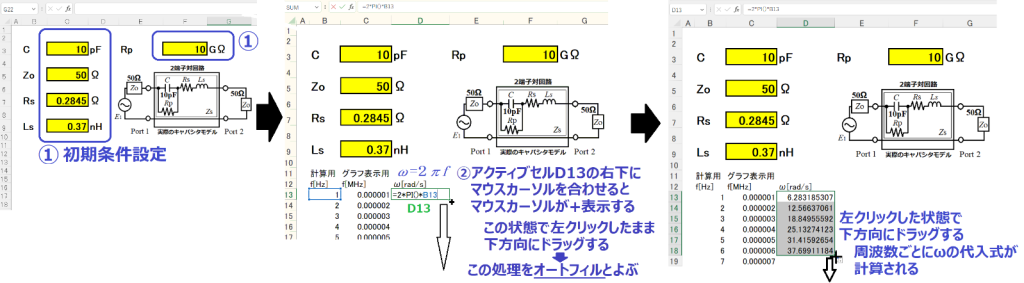
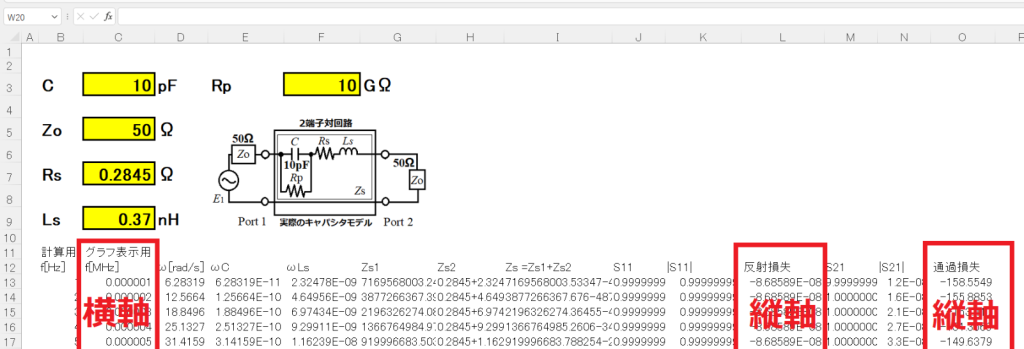
①最初に初期条件設定として、キャパシタCを10pF、ZOを50Ωにします。さらにRsを0.2845Ω、Lsを0.37nH、Rpを10GΩにします。
②つぎに周波数fを記述し、角速度ω( =2 π f )[rad/s]を求めます。
③さらに角速度ωとキャパシタCとの積ωC、角速度ωとインダクタンスLsとの積ωLsを求めます。
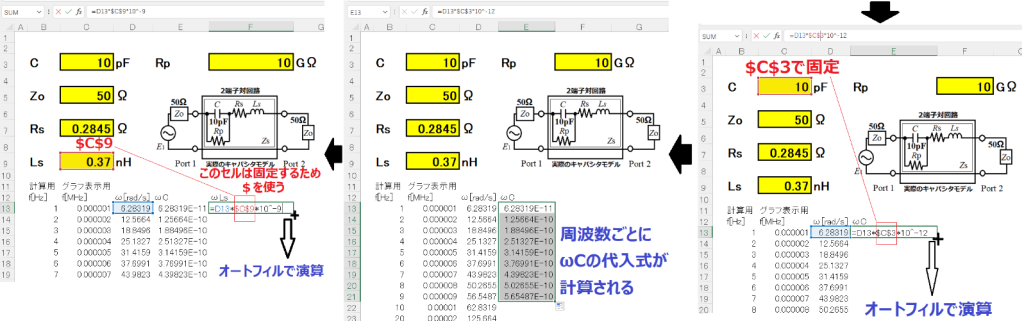
つぎはこの章のメインとなるZsの計算じゃ。
まずはZs1とZs2を複素関数を使って表現してみよう。


Zs1とZs2の式は下のようになります。
それぞれをエクセルを使って複素関数で求めてみます。
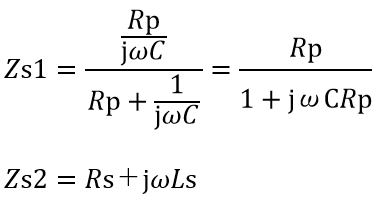

そうじゃな、その調子じゃ。
つぎにZs1とZs2の複素関数の和をとってZsを求めよう。Zsが求まれば、下の式を使ってS11とS21さらには反射損失と通過損失が求まるぞ。

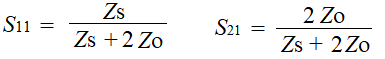
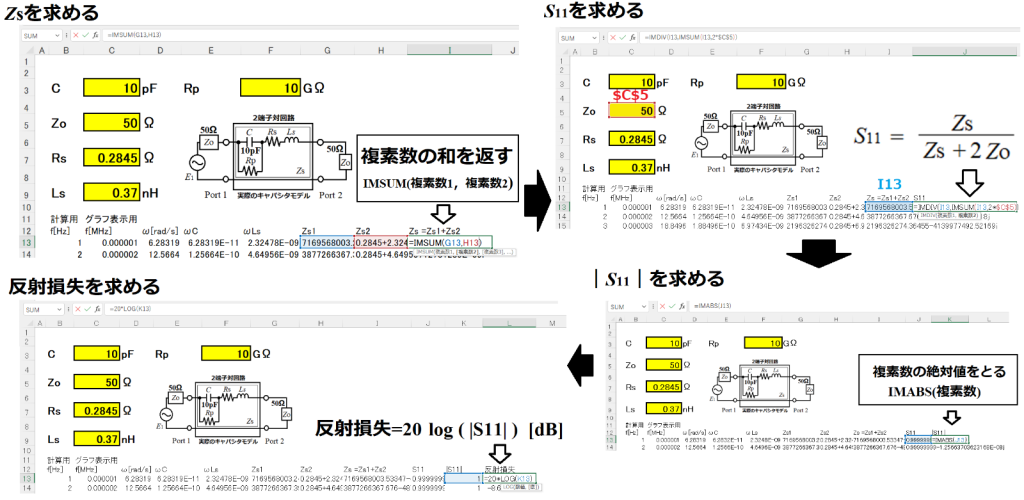

つぎに通過損失を求めます。
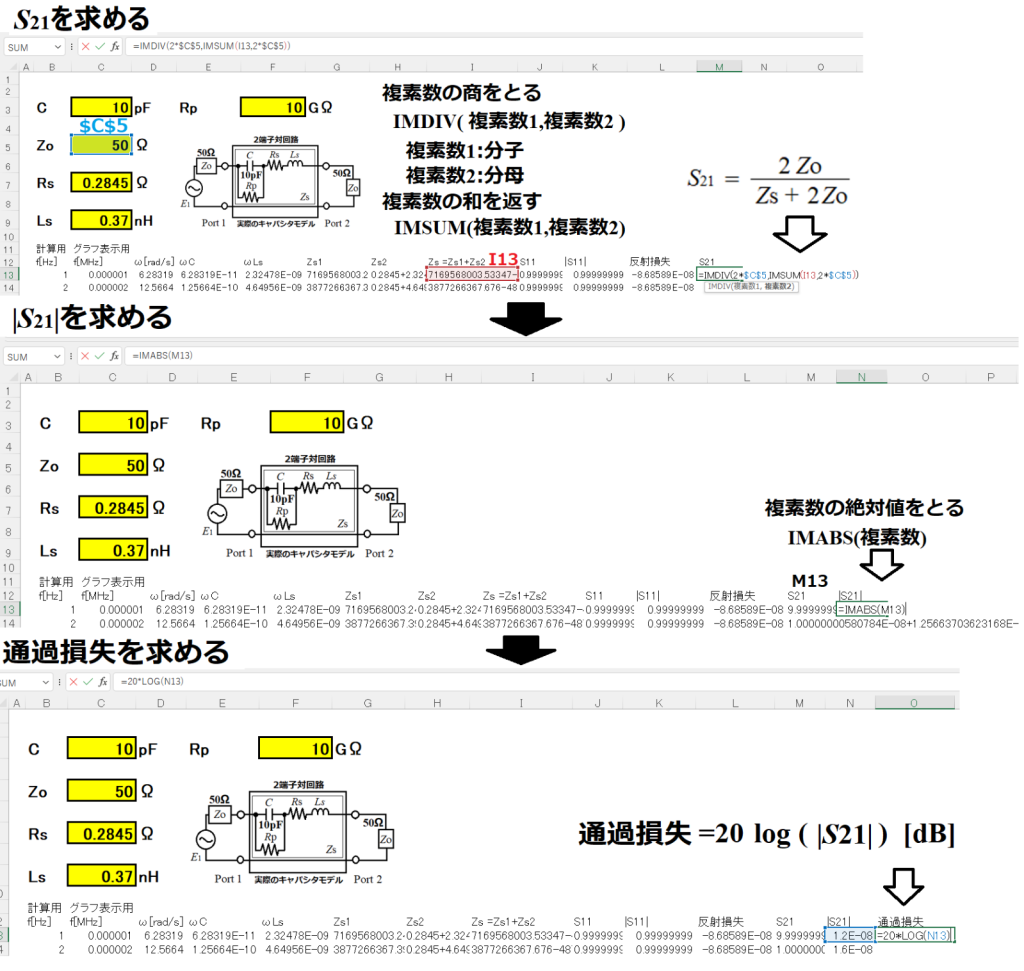

反射損失と通過損失が求まったのでグラフにしました。
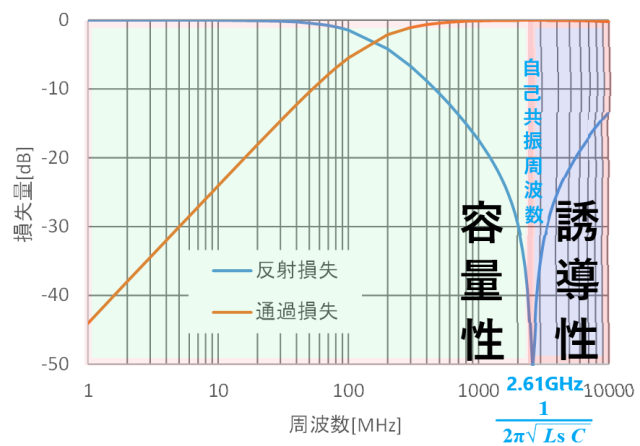
よろしい。ここでは容量Cと等価直列インダクタンスESL(Ls)による共振がみられる。この周波数2.61GHzを自己共振周波数とよんでおる。インピーダンスはこの共振周波数を境に容量性と誘導性に切り替わっておるのじゃ。
これで直列素子のSパラメータの説明は終わりじゃ。
次回から並列素子のSパラメータの説明をしよう。

