
前回(085 EMI対策 ~直列素子のSパラメータ(インダクタ編2)~)では2端子対回路の中にインダクタLを直列接続したときの反射損失と通過損失を求めました。この章では、実際のインダクタLに寄生する浮遊容量CO (ストレーキャパシティーとよぶ)と等価直列抵抗Rs(ESR)と等価並列抵抗Rp(EPR)を想定した場合の反射損失と通過損失を求めます。
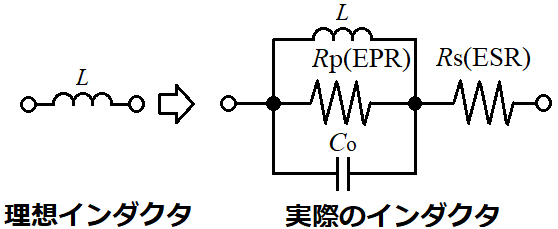

昇平博士、実際のインダクタはL、Rp、Coは並列接続、さらにRsが直列接続しています。
そうじゃな。2端子対回路に実装すると、下のような回路図になる。
この回路によるとS11とS21を求めるには、まずZsを求める必要があるのじゃ。
なみりん、Zsを求めてみよう。

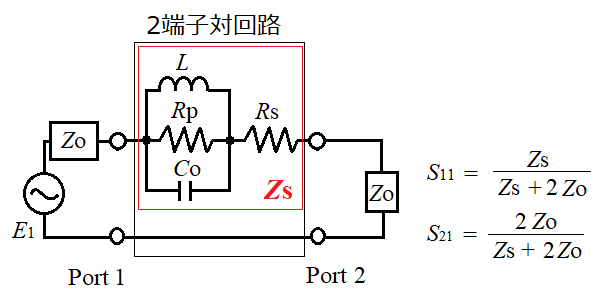

昇平博士、ここでは合成インピーダンスを求めればいいわけですね。
でも、、、、分母に複素数、さらにRsが加算されて複雑な多項式になってしまいました。
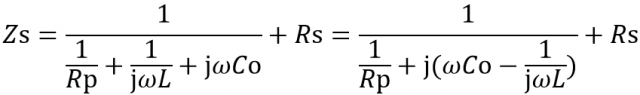
心配しなくてよい、ここから、Excelの複素関数を使って計算するのじゃ。
ZSが求まったら、そのまま複素関数を使ってS11とS21を求めてみるのじゃ。
では順番に演習するぞ。
①インダクタL、等価並列抵抗Rp、ストレーキャパシティCO、等価直列抵抗Rs、特性インピー ダンスZOに任意値が入力できるようにしよう。ここではLは10nH、Rp(EPR)は9000Ω、ストレーキャパシティCOは0.219pF、Rs(ESR)は0.22Ω、特性インピーダンスZOは50Ωとしよう。
②つぎに周波数fを記述し、角速度ω( 2 π f )[rad/s]を求めておこう。

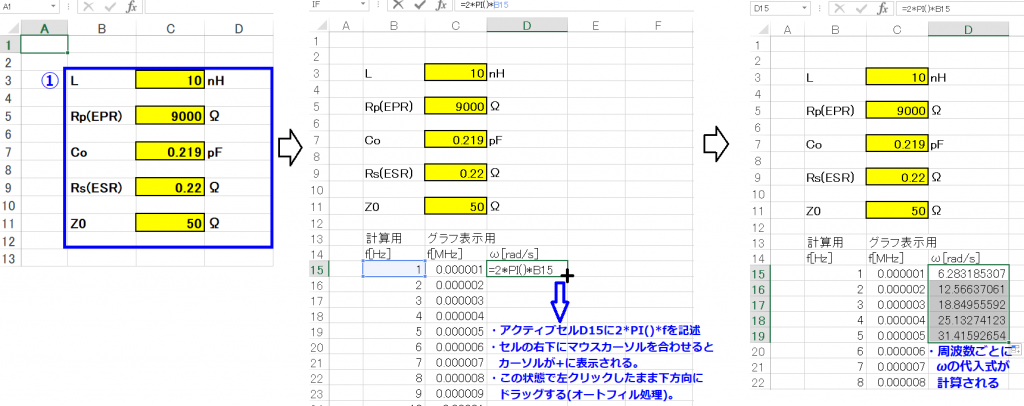
③つぎはωLとωCOを求める。
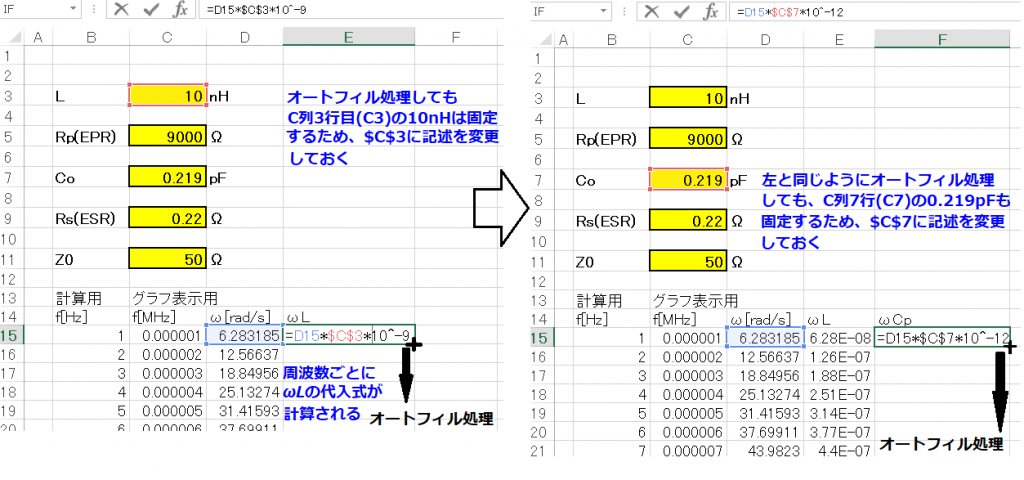
オートフィル処理を行うときに、周波数が変化してもインダクタLは固定しておきたいので、セル C3は $C$3 に記載変更した後でオートフィル処理を行うとよい。
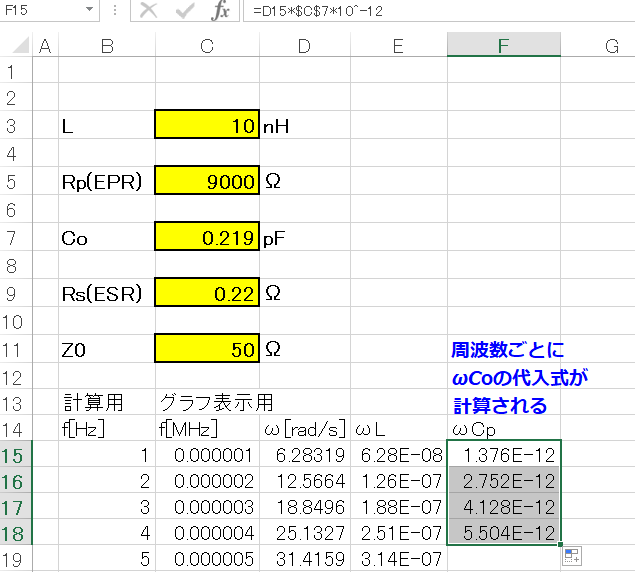
ストレーキャパシティCOも同じようにセルC7 を $C$7 に記載変更した後でオートフィル処理を行うのじゃ。


昇平博士、つぎはZSの計算ですね。
④Zsの式が長いので分数項を先に計算しておき(Zpとする)、あとでRsを加算してみよう。

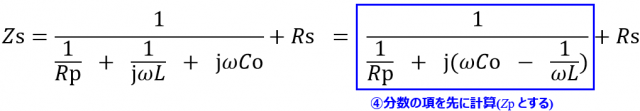

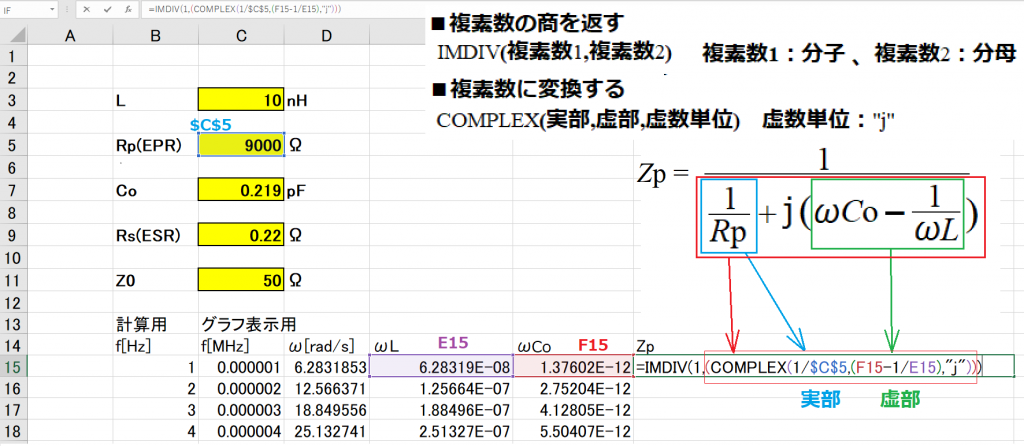
Zpを複素関数を使って式を作ってみました。Zpの分母は実数と虚数にまとめておきCOMPLEXを使います。その結果をもとにIMDIVで複素数の逆数を取ります。

Zsは、Zp+Rsなので、IMSUMを使って計算します。
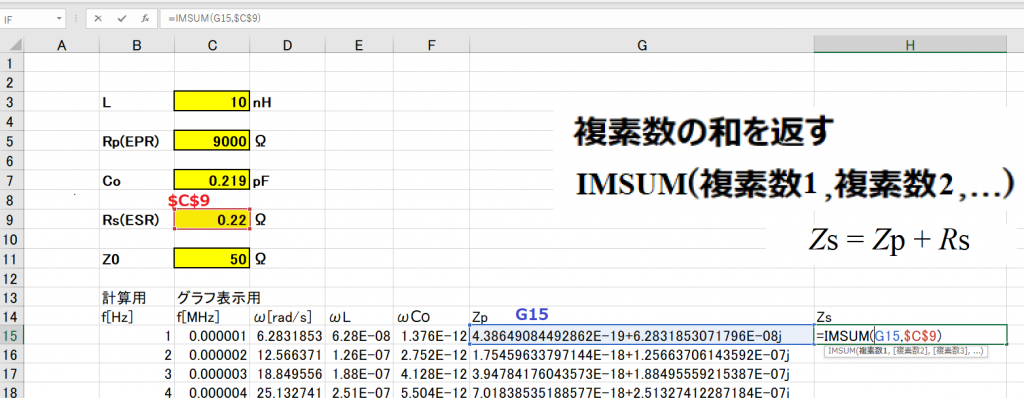
⑤Zsが求まったので、S11とS21が計算できる状態になったな。
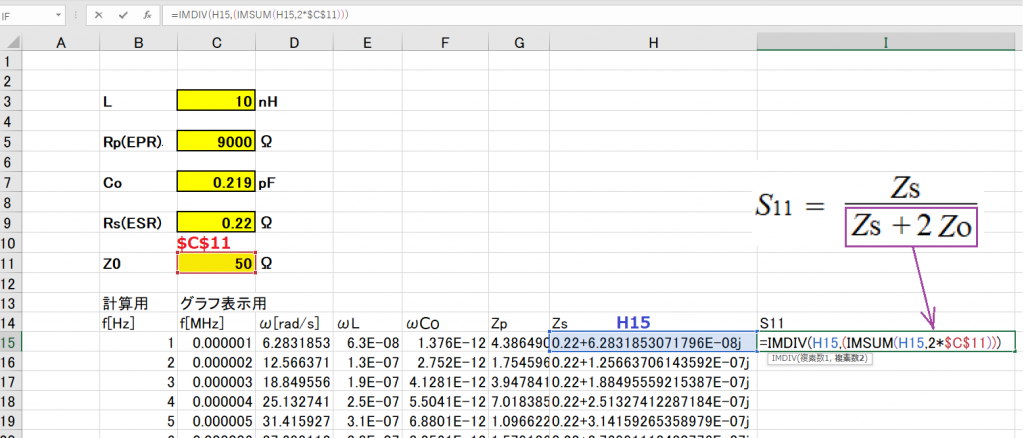
以下のとおり、複素関数でS11が求まった。
なみりん、反射損失を求めるのじゃ。


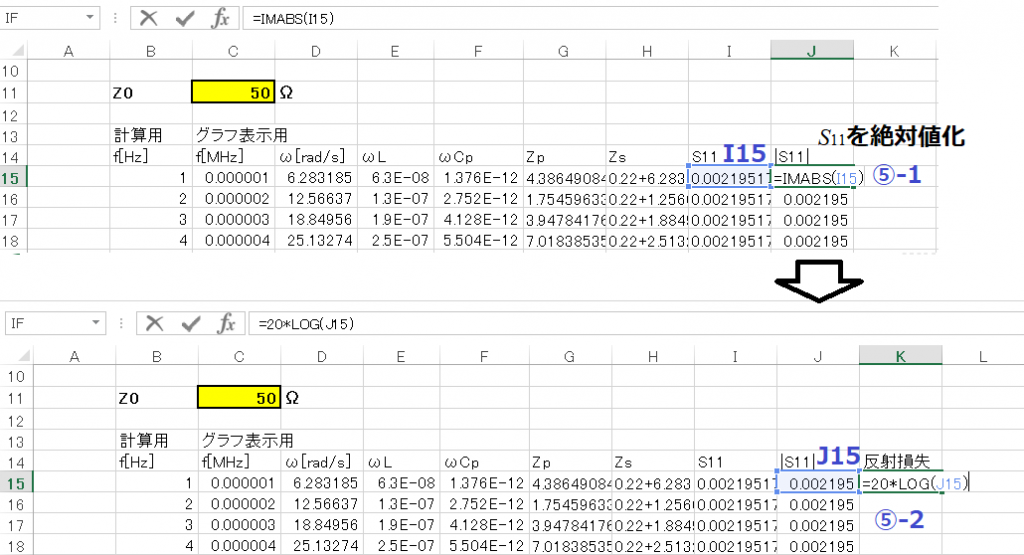
⑤-1 複素数のS11を絶対値化するためにIMABSを使って、絶対値|S11|に変換します。
⑤-2 つぎに反射損失を求めます。反射損失 = 20 log ( |S11| ) [dB]
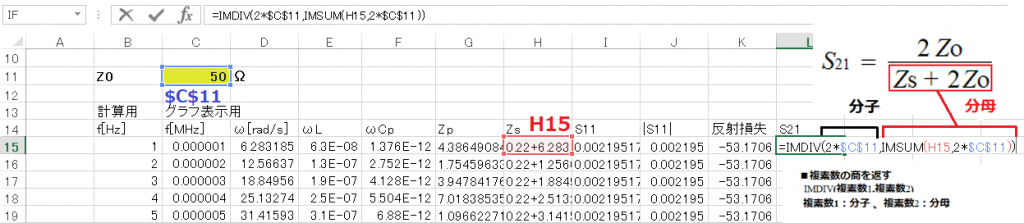
つぎは通過損失を求める前に、以下のようにS21を求めておく。
なみりんよ、通過損失を求めグラフにしてみるのじゃ。


反射損失と同じように求めればいいわけですね。
複素数のS21を絶対値化するためにIMABSを使って、絶対値|S21|に変換します。
つぎに通過損失を求めます。通過損失 = 20 log ( |S21| ) [dB]
通過損失が求まったので横軸に周波数、縦軸に反射損失と通過損失のグラフを示します。
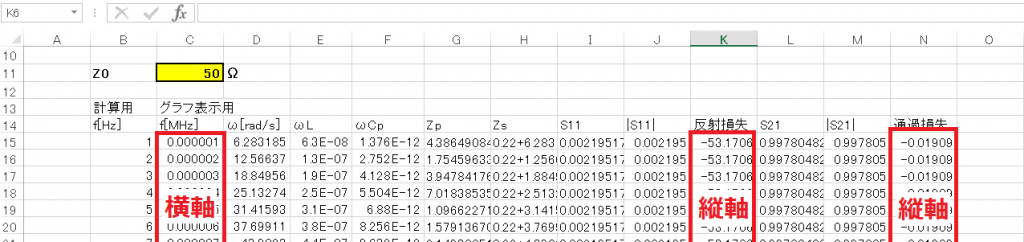
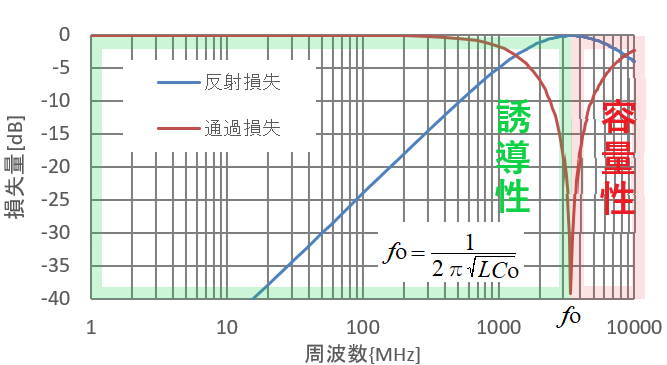
よろしい。これが直列接続した時の実際のインダクタLの反射損失と通過損失である。
インダクタLとストレーキャパシティCOで構成された共振現象があり3.4GHzで深い減衰がみられる。このときの周波数fOを自己共振周波数とよんでおる。


自己共振周波数fOは、L=10nH、CO=0.219pFなので、自己共振周波数はグラフに記載された式から3.4GHzになるわけですね。
そのとおりじゃ、自己共振周波数fOより低い周波数ではインダクタとして機能(誘導性)するが、自己共振周波数fOより高い周波数ではキャパシタと機能(容量性)することになる。
以前紹介した #047 EMI対策 ~フィルタ(インダクタ その1)~では概要だったが、今回はさらに詳細を説明した。なみりん、分かったかな。
次回は直列素子のSパラメータ(キャパシタ編)についてお話しよう。

