
前回(#083 EMI対策 ~ Sパラメータ その2 ~)では以下のような式を求めました。
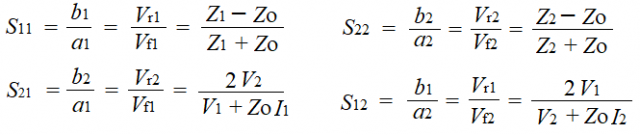
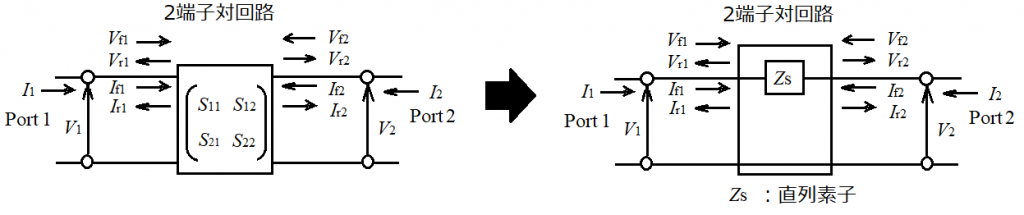
今回は、2端子対回路に直列素子ZSを入れたときのSパラメータを求めよう。


昇平博士、どうやって求めればよいですか。
まずS11とS21を求めようと思うのじゃが、下のように回路図にすると分かりやすくなるぞ。
Port1からPort2側を見たとき、Z1は何が見えるかの?

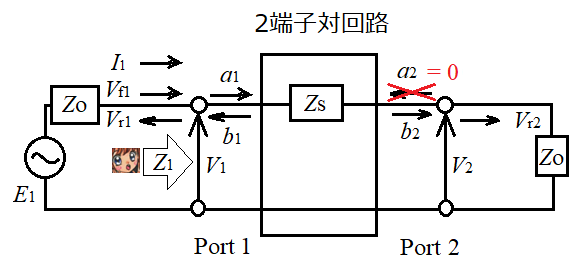

Z1は、直列素子Zsと負荷ZOの和ですね。
S11はもう求まってしまったわ。
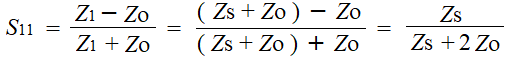
よろしい。
ではS21はどうなるかの?


V2はPort2の負荷ZOとI1の積で求まりますね。
V1はZ1(= Zs + ZO )とI1の積なので、( Zs + ZO ) × I1です。結果、S21は下のようになりました。
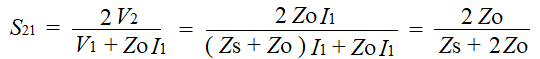
残りのS22とS12も同じように求めればよい、下の回路図にすると分かりやすくなるぞ。
Port2からPort1側を見たとき、Z2は何が見えるかの?

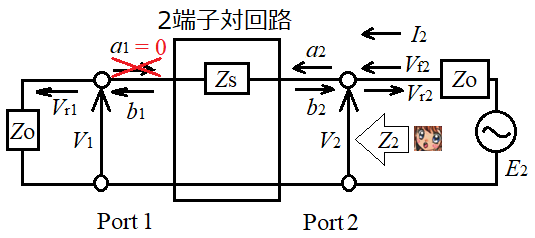

Z2は直列素子Zsと負荷ZOの和ですね。
あらー。S11=S22、S21=S12が成立しますね。
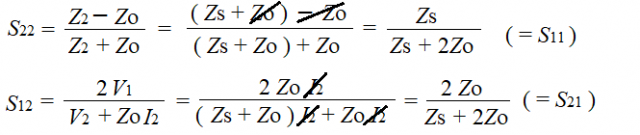
なみりん、そうじゃな。
では、ZsにインダクタLを入れて、S11とS21を求めてみようか。
S22とS12は、S11とS21と同じなので省略する。

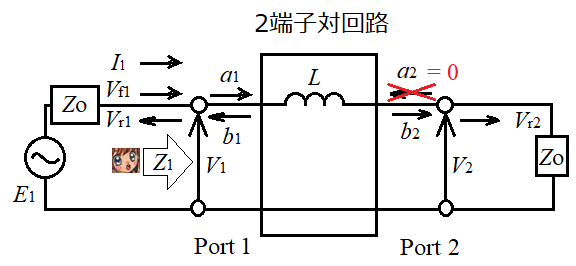

インダクタLはインピーダンスで表現すると、Zs = jωLなので、、、
以下のようになります。虚数jが混在してて面倒だわ。
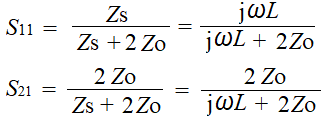
なみりんよ、以前使ったExcelの複素関数を利用するとよい。
共役複素数を分母分子に掛けて(複素数の有理化)、実数と虚数に分ける面倒な作業は不要じゃ。
まず最初に、Excelを起動しておき、
ファイル>オプション>アドイン>設定(G)… に進み、分析ツールにチェックを入れておこう。
以下によく使う関数をまとめて記載しておこう。



例えばS11、S21は下のように記述していくのですね。
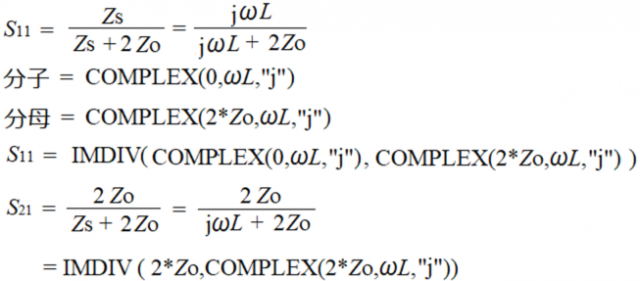
そうじゃな。
この結果をもとに横軸を周波数[MHz]、縦軸をリターンロスと通過損失のグラフが出来る。
グラフ作成までの過程は次回に説明しよう。

