#73ではキャパシタとインダクタを使ってイミッタンスチャート上で、あるインピーダンスを所望のインピーダンスへ移動した。
いわゆる集中定数回路でのインピーダンス変換を説明した。覚えてるかな？
はい。覚えていますよ。
今回はマイクロストリップ線路によるインピーダンス変換をスミスチャート上で説明しよう。
マイクロストリップ線路って何ですか？
よし。では最初にマイクロストリップ線路の説明じゃ。
誘電体基板の裏面全体がグランド面となるように導体パターンを形成し、表面に線上の導体パターンを形成した構造の電磁波を伝達する伝送路じゃ。
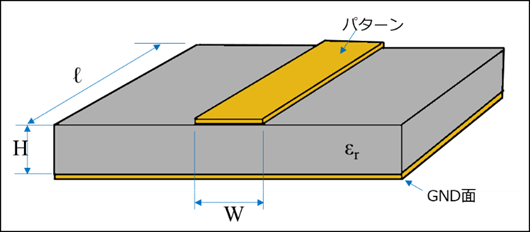
誘電体の厚みをH、比誘電率をεrとし、表面パターンの幅をW、長さを
とする。
このとき、このマイクロストリップ線路の特性インピーダンスZ0と波長短縮率
は以下の近似式で表すことができるのじゃ。
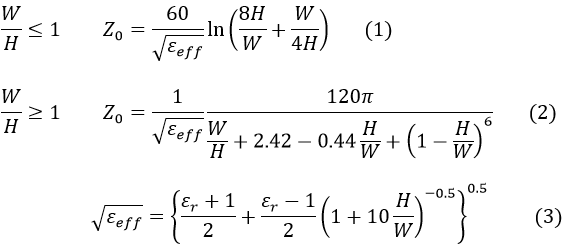
結構面倒な計算ですね。電卓で計算するのは厳しいですね。
前回までの説明で、スミスチャートは特性インピーダンスZ0で正規化されたチャートであることを説明した。従ってこのマイクロストリップ線路の特性インピーダンスZ0で正規化されたチャートにプロットされるのじゃ。
あっ！#70で教えていただいたスミスチャートの説明ですね！
やっとスミスチャートが出てきましたね。
なみりん。よくぞ覚えていてくれたのぉ。
そぉじゃ。それから、線路長が半波長毎に反射ベクトルは時計回りに一回転するのじゃ。つまり、360°回転するのじゃ。
では、ここから具体例で説明するぞ。
下図のようにZ1のインピーダンスにマイクロストリップ線路を接続したときの変換されたインピーダンスZ2をスミスチャートで求めるぞ。
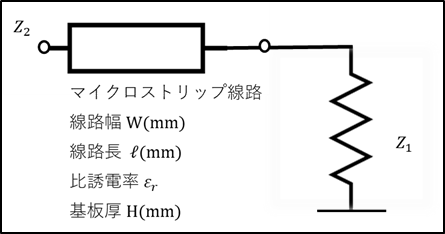
はい。
下表のように、いろんなZ1、誘電体基板、マイクロストリップ線路のパターン、想定周波数でどうなるかを考えてみる。ってことですね。
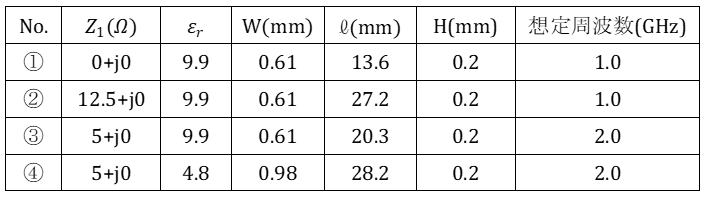
いずれの場合も
なので、前述の(2)式からZ0を求めることができるのじゃ。また、(3)式から波長短縮率を求めることができるのじゃ。
それらが以下の表となるのじゃ。
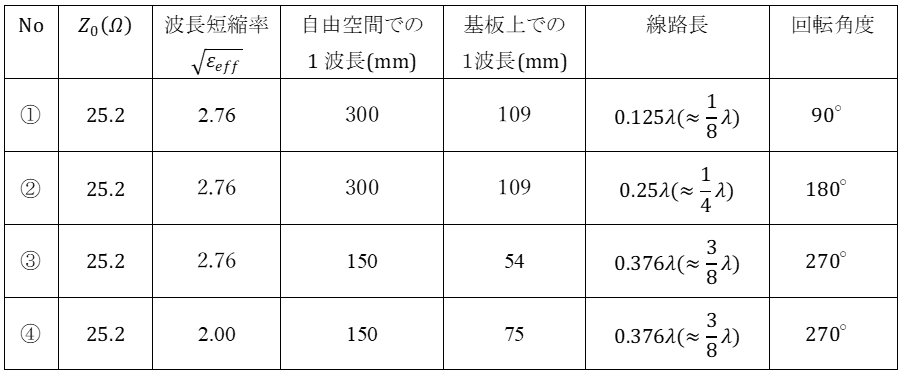
博士！ 表の数値をちょっと確認させてください。
Z0と
は上の(2)式、(3)式から求められることわかりました。
自由空間長での1波長は
なので、①②の場合は３ × 1011 ⁄ 1 × 109 = 300 (mm)ですね？
基板上での１波長は自由空間での1波長/波長短縮率なので、①の場合は300 / 2.76 = 109 (mm)ですね？
線路長は①の場合、
なので
でよいですか？
回転角度は
で360°なので①の場合、
なので90°ですね。
なみりん。
そのとおりじゃ。
これらをZ0 = 25.2 (Ω)で正規化されたスミスチャートで表すと以下の図となるのじゃ。
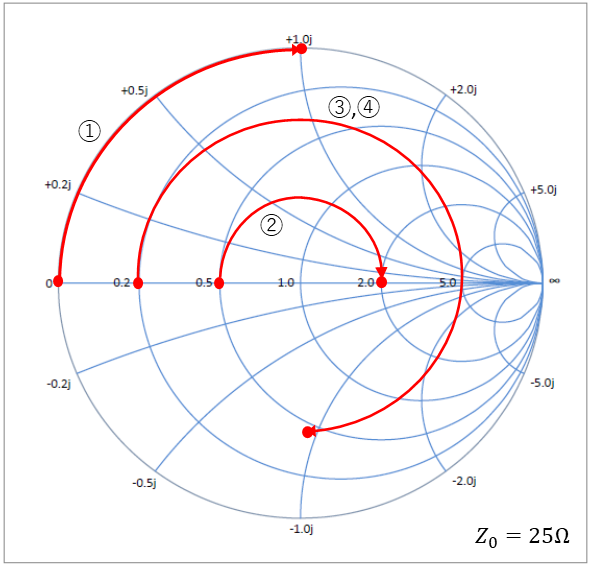
①はショート点から1 + j0を中心に90°時計回りに動き、z2 = 0 + j1.0へ移動するのじゃ。
②はz1 = 0.5 + j0から1 + j0を中心に180°時計回りに動き、z2 = 2 + j0へ移動する。1/4 λの線路長の場合、実軸上でインピーダンス変換が可能となる。この場合、12.5 Ωから50 Ωへ変換されるのじゃ。
ちなみにZ1を50 Ωへインピーダンス変換したい場合、マイクロストリップラインのZ0は
で求められるぞ。
③はz1 = 0.2 + j0から1 + j0を中心に270°時計回りに動き、z2 = 0.38 - j0.92へ移動するのじゃ。
④は③と基板もパターンも異なるが、Z0も回転角も同じなので同じ軌跡を描くのじゃ。
今回の説明はここまでじゃ。
なみりん。マイクロストリップ線路でのインピーダンス変換を理解できたかな？
はい。よーくわかりました。
ありがとうございました。