今回は今までの応用例として、あるインピーダンスを所望のインピーダンスへ動かしてみよう。


はい。よろしくお願いします。
今回の事例として、z1 = 0.5 + j1.0(y1 = 0.4 - j0.8)-図中の▲の点をz2 = 1.0 + j0(y2 = 1.0 + j0)-図中の●の点へ移動させてみよう。また想定周波数を1GHzとし、二つのコンデンサまたはコイルを使って移動させるぞ。二つの部品で移動させる場合、何通りかの軌跡が考えられる。四つの軌跡の事例を紹介しよう。


はい!? 前回教えていただいた抵抗は使わないんですか?
高周波の場合、抵抗を使ってインピーダンスを移動させると、損失となるので、抵抗を使わないでインピーダンスを移動させることが普通なんじゃ。


そうなんですね。わかりました。
まず、最初の軌跡じゃ。
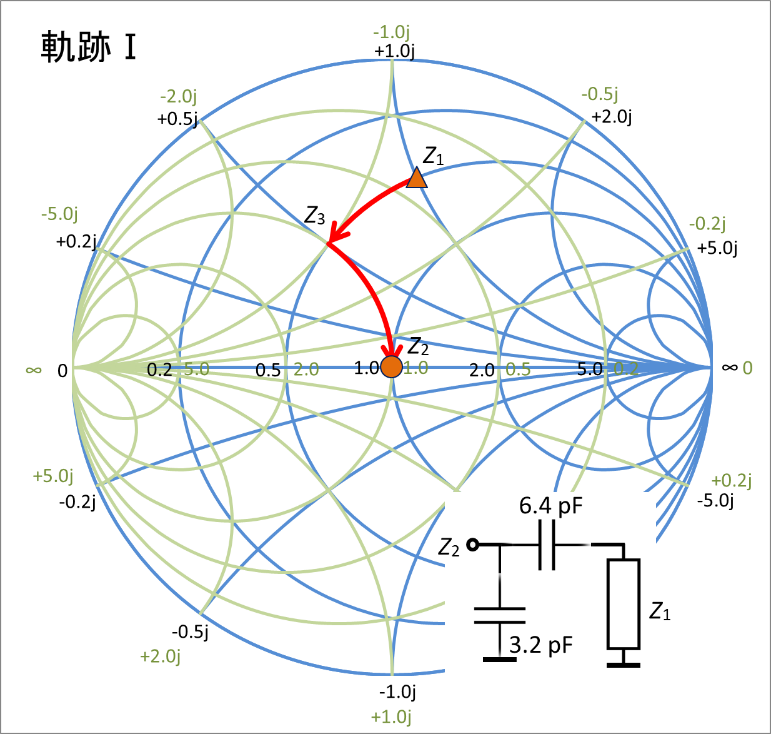
直列のCを接続することで等抵抗円上を反時計回りにz3(0.5 + j0.5)まで動くのじゃ。このときリアクタンスは+1.0jから+0.5jへ移動する。そのCの値は6.4pFじゃ。
その後並列のCを接続することで等コンダクタンス円上を時計回りにy3(1.0 - j1.0)からy2(1.0 + j0)まで動くのじゃ。このときのサセプタンスが-1.0jから0jへ移動する。そのCの値は3.2pFじゃ。
つまり直列の6.4pFのコンデンサと並列の3.2pFのコンデンサを接続することで、z1のインピーダンスをz2へ移動させることができるのじゃ。


なるほど。スミスチャートって便利ですね。
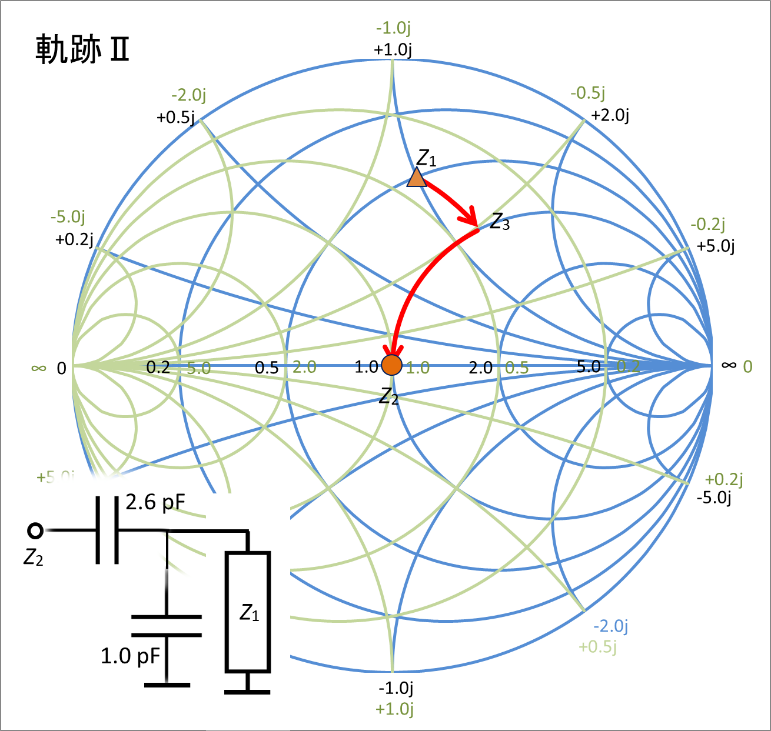
続いて二つ目の軌跡じゃ。まず、並列のCで等コンダクタンス円上を時計回りに動くのじゃ。y1(0.4 - j0.8)からy3(0.4 - j0.49)への移動はサセプタンスが-0.8jから-0.49jへ移動する。そのCの値は1pFじゃ。
その後 直列のCで等抵抗円上を反時計回りに動くのじゃ。z3(1.0 + j1.225)からz2(1.0 + j0)への移動はリアクタンスが+1.225jから0jへ移動する。そのCの値は2.6pFじゃ。
つまり並列の1pFのコンデンサと直列の2.6pFのコンデンサを接続することで、z1のインピーダンスをz2へ移動させることができるのじゃ。

どんどん行くぞ。三つ目の軌跡じゃ。
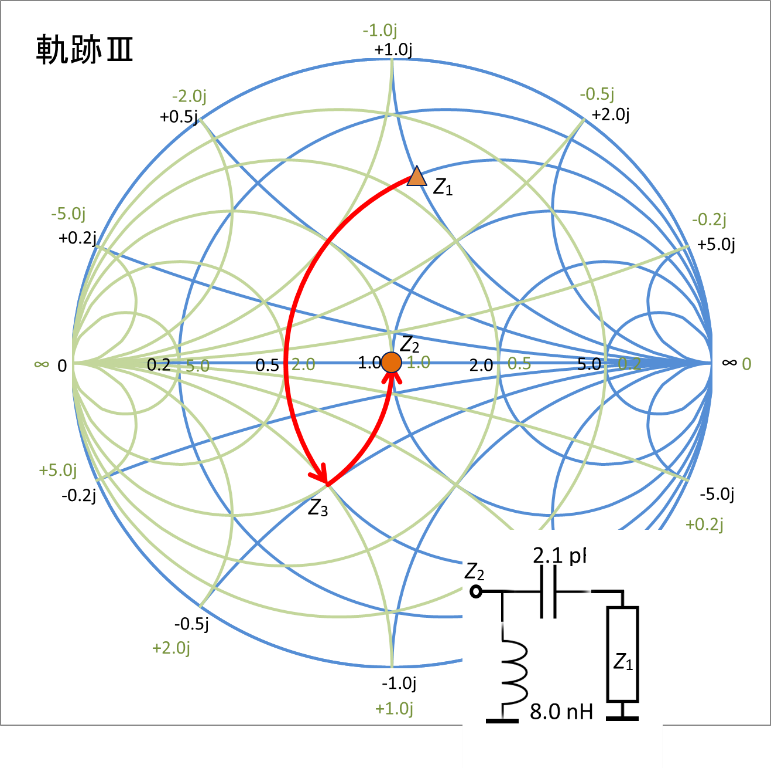
まず、直列のCで等抵抗円上を反時計回りに動くのじゃ。z1(0.5 + j1.0)からz3(0.5 - j0.5)への移動はリアクタンスが+1.0jから-0.5jへ移動する。そのCの値は2.1pFじゃ。
その後並列のLで等コンダクタンス円上を反時計回りに動くのじゃ。y3(1.0 + j1.0)からy2(1.0 + j0)への移動はサセプタンスが+1.0jから0jへ移動する。そのLの値は8.0nHじゃ。
つまり直列の2.1pFのコンデンサと並列の8.0nHのコイルを接続することで、z1のインピーダンスをz2へ移動させることができるのじゃ。


ちょっと待ってください。ついていけなーい!
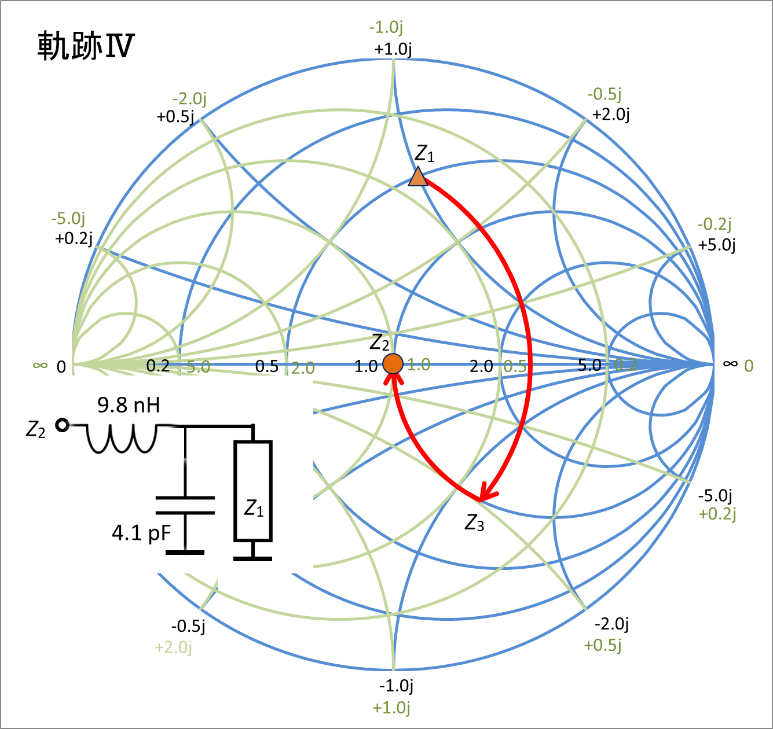
まだまだ!四つ目の軌跡じゃ。まず並列のCで等コンダクタンス円上を時計回りに動くのじゃ。y1(0.4 - j0.8)からy3(0.4 + j0.49)への移動はサセプタンスが-0.8jから+0.49jへ移動する。そのCの値は4.1pFじゃ。
その後直列のLで等抵抗円上を時計回りに動くのじゃ。z3(1 - j1.225)からz2(1 + j0)への移動はリアクタンスが-1.225jから0jへ移動する。そのLの値は9.8nHじゃ。
つまり並列の4.1pFのコンデンサと直列の9.8nHのコイルを接続することで、z1のインピーダンスをz2へ移動させることができるのじゃ。

今回の説明は以上じゃ。
どうじゃ?なみりん。わかったかのぉ?


はい!スミスチャートの便利なのがわかりました。
もう一度復習しておきまーす!
ありがとうございました。
