
今回も引き続き、キャパシタの共振のお話です。
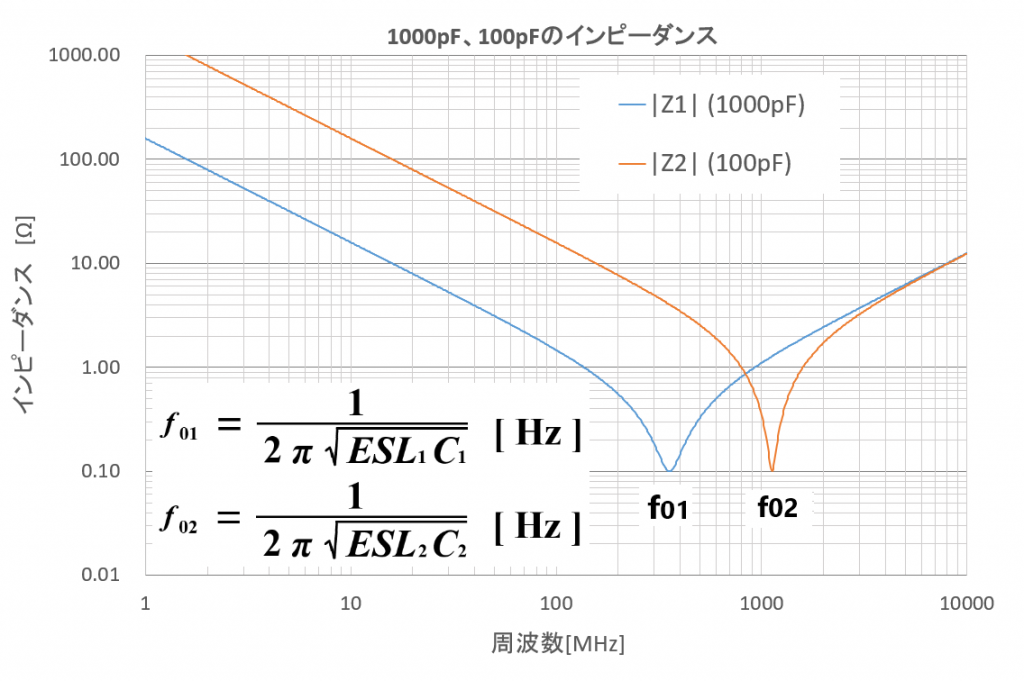
前回はZ1とZ2の絶対値|Z1|と|Z2|を求めたので、今回は周波数を横軸に、インピーダンスを縦軸にしたときの|Z1|と|Z2|をグラフで表現してみよう。

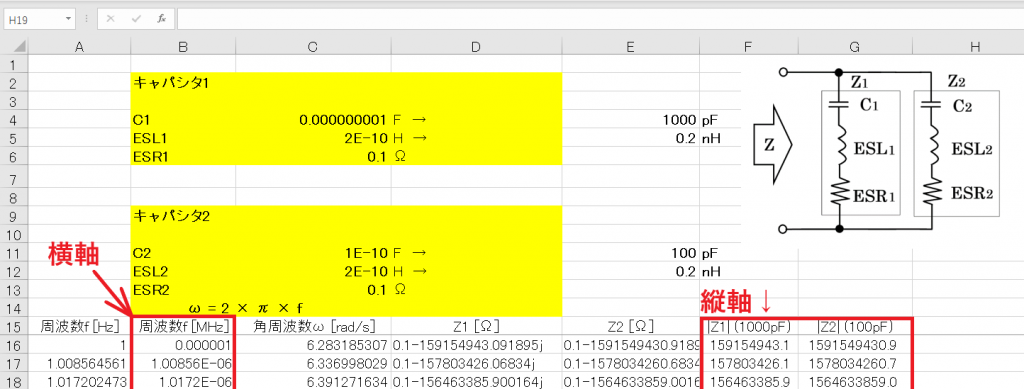

下にインピーダンスの周波数特性を示します。
Z1の自己共振周波数f01は、355.88MHz
Z2の自己共振周波数f02は、1.125GHzです。
そうじゃな。
次は1/Z1と1/Z2をそれぞれ求めよう。ここで使う複素関数は、
③複素数の商を返す
IMDIV(複素数1,複素数2)
複素数1:分子 複素数2:分母

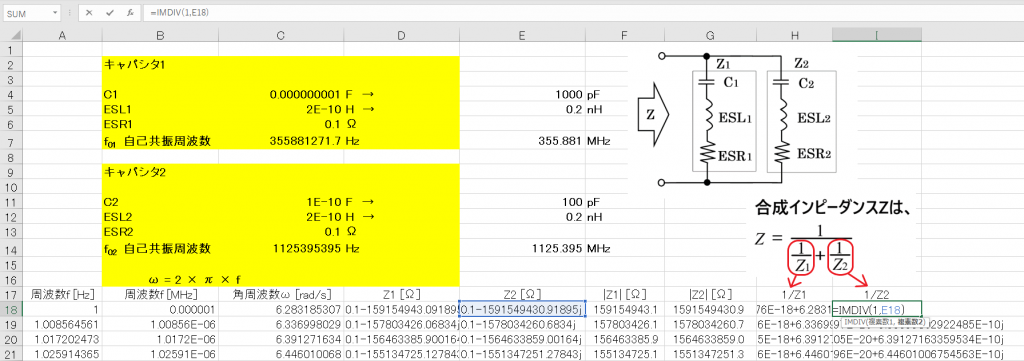
次は1/Z1と1/Z2の和を求めよう。ここでは使う複素関数は、
④複素数の和を返す
IMSUM(複素数1,複素数2,...)
最後は、1/Z1と1/Z2の和の逆数をとるのじゃ。これが求める合成インピーダンスになる。

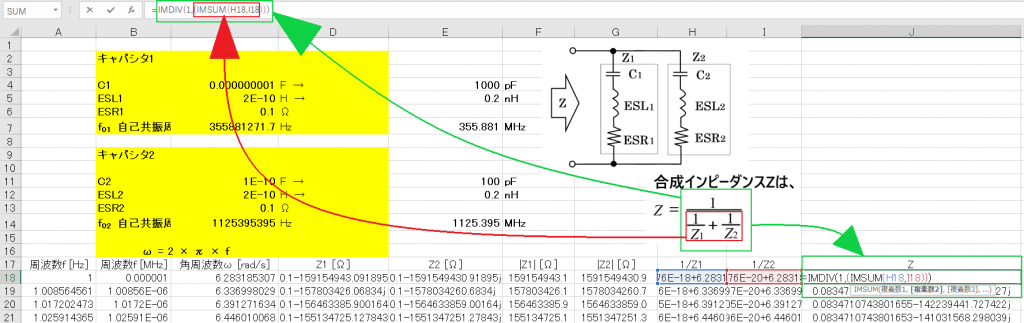

これで合成インピーダンスZが求まったわね。
あとは、複素関数IMABSでZの絶対値を求めればグラフ化できるわけですね。
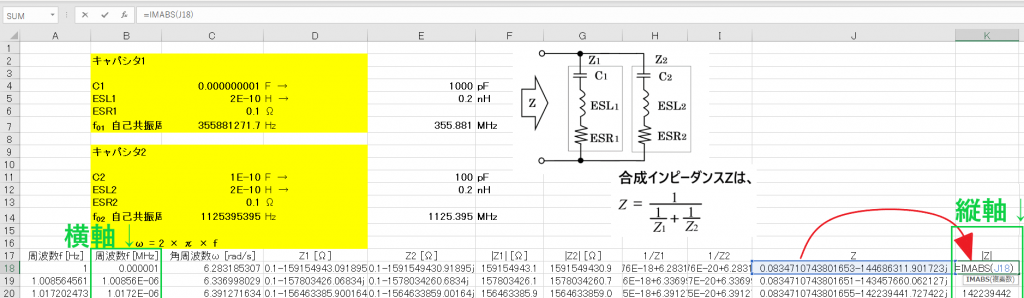
そういうことじゃ。
合成インピーダンスZを追加したときのグラフを下に示そう。
Z2の自己共振周波数の直前にインピーダンスが急激に高くなっておるが、これを反共振とよぶ。
反共振周波数を求める式もグラフに書き込んでおこう。

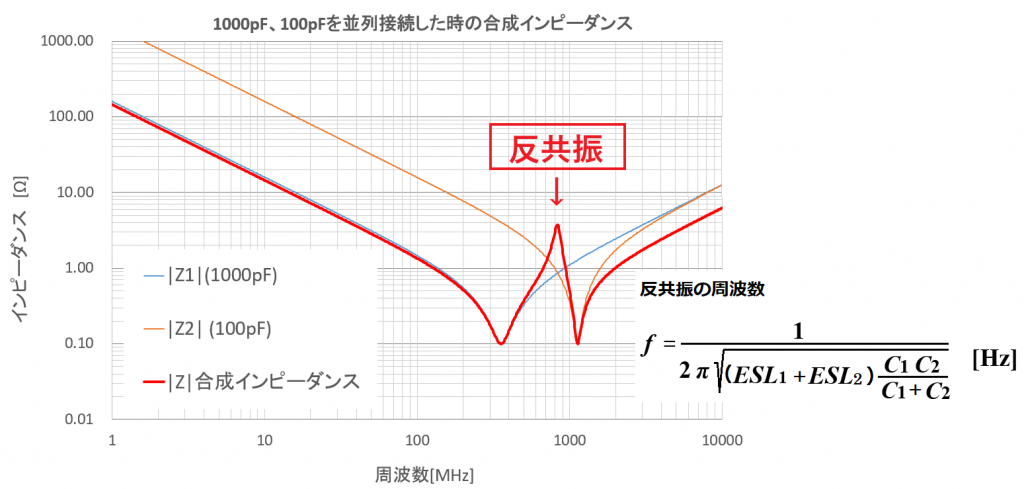

昇平博士、反共振周波数は834.61MHzになりました。
反共振周波数のインピーダンスが高いと、ノイズが吸収できなくなるので
インピーダンスは低い方がいいわけですよね?
もちろん、そういうことになる。
次回は、実際にこの計算ツールと使って反共振の検討をしてみよう。
なみりん、念願の合成インピーダンスを求める計算ツールができたな。
時間があれば、キャパシタ3つを並列接続したときの計算ツールを作ってみるのじゃ。インピーダンスの振る舞いをイメージするのに便利じゃぞ。


次回も引き続き、キャパシタの共振のお話です。
