株式会社Wave Technology 営業部です。
「電磁気学は苦手」と感じている人はおられませんか？
理系であれば高校の物理でも初歩レベルを学習しますし、大学で電磁気の授業を受けた人も少なからずおられるはずですが、電磁気を苦手と感じている人は少なくないようです。
電磁気の苦手意識を克服し、むしろ面白く感じるためには、数式をイメージで捉えることも大切なことだと思います。そのことをガウスの定理を使って、今回ご紹介させていただきますね。
【ガウスの定理】積分形の意味をイメージしてみましょう
ガウスの定理の積分形は、以下の式で表されます。
∲s E・dS =q/ε0 （１）
今回の提案は、この式の意味を以下のようにイメージしてみましょうということなんです。
① 電荷は電気力線を出す
② 電荷qが出す電気力線の本数はq/ε0である
③ 単位面積当たりの電気力線の本数が電界である
④ 電荷から出た電気力線は、無限遠、又は、反対電荷に向かって伸びる
（電気力線の矢印の向きは、プラス電荷→マイナス電荷/無限遠、無限遠→マイナス電荷）
以上のイメージを使って、図１を眺めてみましょう。
電荷qがガウス面Sの中にある場合のイメージ
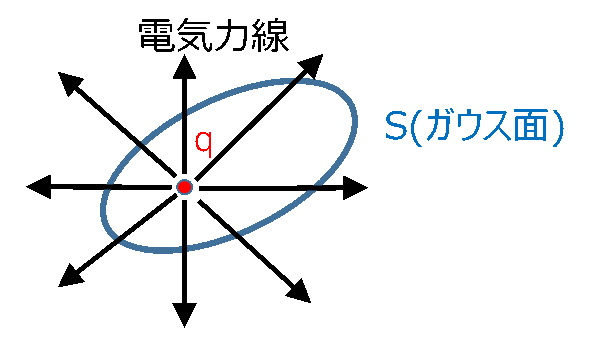
図１. 電荷qがガウス面Sの中にある場合
図中に電荷qがありますので、この電荷が出す電気力線の本数は、上記①、②より、q/ε0 本となります。
それではここで質問です。
Ｑ： ガウス面Sを貫通する電気力線を数えたら、何本になるでしょうか？
Ａ： ②より、もちろん、q/ε0 本ですよね。
以上で、ガウスの定理の説明がすべて終了しました（笑）
あっけなく終わってしまいましたので、もう少し詳しく見ていきましょう。
上記の質問の「ガウス面Sを貫通する電気力線を全部数えたら」が式（１）の左辺で、その答えの「q/ε0 本です」が、式（１）の右辺なのです。
左辺でやっていることは、任意のガウス面Ｓ上での電界の面積分ですよね。
一方、③より、電界は単位面積当たりの電気力線の本数です。
ということは、∲s E・dS が表わしていることは、ガウス面上の単位面積当たりの電気力線の本数を面積積分しているということ、つまり、電荷から出ている全ての電気力線の本数を数えているのです。
そして、電荷qが出す電気力線の本数は、q/ε0 本ですので、それが（１）の右辺になっているということなのです。
左辺で電気力線の本数を数えて、右辺がその本数の答え、というただそれだけの式です。
もし、電荷qが出した電気力線のうち、ガウス面内に留まるものがあった場合は、こうはいきませんよね。そうなれば、電気力線は全て数えたことになりませんから。
でもご安心ください。それはありません。
電荷から出た電気力線は、無限遠、又は、反対電荷に向かって伸びていく(④)ことを考えれば、電荷qから出た電気力線の全てがガウス面Sを貫通することは明らかです。
ここまでわかったところで次に、以下の図のような場合、式（１）はどう表現されるのか？ そして、電気力線で考えるとどうなるのか？ 皆さんで考えてみてくださいね。
電気力線を出す電荷がガウス面の中になければどうなるのか、ということですよ。
電荷qがガウス面Sの外にある場合のイメージ
図２．電荷qがガウス面Sの外にある場合
【ガウスの定理】についてイメージできましたでしょうか？
今日はこの辺で。
電気・電子の勉強には、汲めども尽きない面白みがあります。
当社では、テクノシェルパのブランド名称で、実践的な電気・電子に関する講座を開催しています。
【テクノシェルパ各講座】
【関連ブログ】
WTIメールマガジンの配信（無料）