
今回は、集中定数と分布定数のお話です。
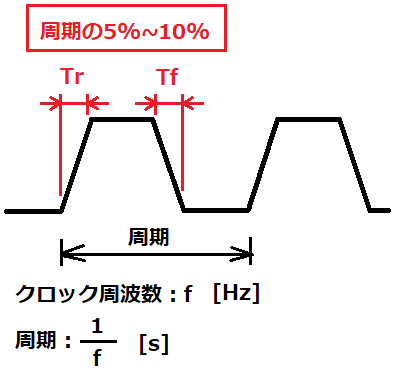 CPUとデバイス間の通信の大部分は、クロック信号(矩形波)に同期したデータを出力して通信を行っており、クロック信号の状態遷移である立下りTrまたは立下りTfは、クロック周期の5%~10%であることが多い。
CPUとデバイス間の通信の大部分は、クロック信号(矩形波)に同期したデータを出力して通信を行っており、クロック信号の状態遷移である立下りTrまたは立下りTfは、クロック周期の5%~10%であることが多い。
例えば、クロック信号が50MHzであれば、その周期は20nsなのでTr、Tfに相当する5%は1ns、10%だと2nsになる。
前回、線路長20cm時のストリップ線路とマイクロストリップ線路の到達時間を求めたけど、今度は50cmの時の到達時間を求めてくれないか?


はい。
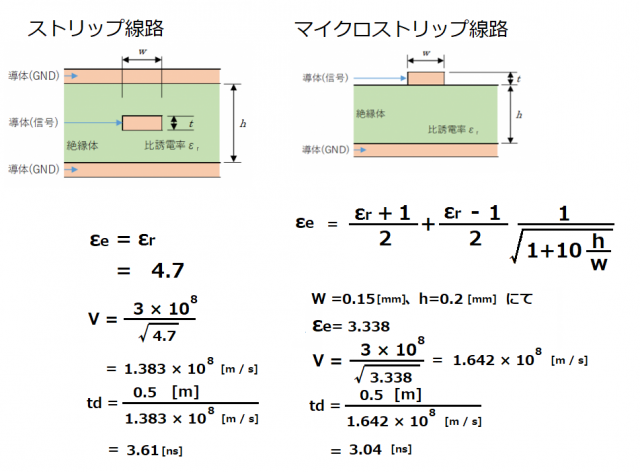
線路長50cmだとストリップ線路は3.61nsで、
マイクロストリップ線路は3.04nsです。
線路長が20cmから50cmへの増加分が
そのまま到達時間にも反映されます。
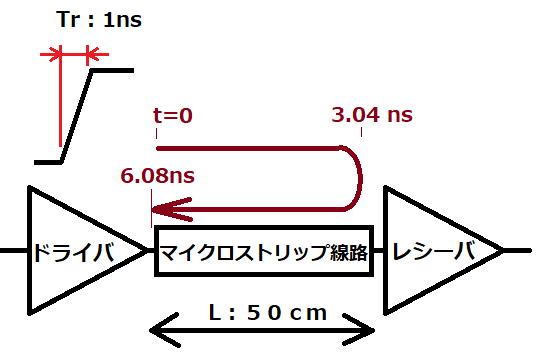
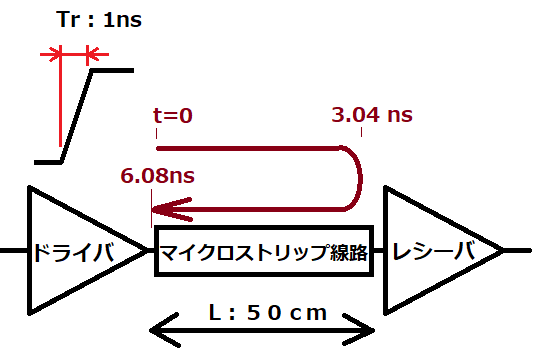 今回は線路長50cmのマイクロストリップ線路で話を続けよう。右の図は、線路長50cmのマイクロストリップ線路の一方にTrが1nsで出力するドライバを接続し、他方にはレシーバを接続している。
今回は線路長50cmのマイクロストリップ線路で話を続けよう。右の図は、線路長50cmのマイクロストリップ線路の一方にTrが1nsで出力するドライバを接続し、他方にはレシーバを接続している。
ドライバから1nsの立上り信号が出力後、3.04ns経過後レシーバの入力端がLoからHiに切り替わる。さらにレシーバを往復してドライバに戻るとさらに同じ時間(往復時間:6.08ns)を要することになる。
この時間の経過とともに、立上り・立下り信号がレシーバに向かって徐々に進行する線路のことを「分布定数線路」とよぶのじゃ。


高周波では分布定数をよく耳にするけど、デジタル回路でもクロックの立上りや立下りが急峻になると分布定数として取り扱うんですね。
分布定数に対して、線路が集中定数だった場合、どのような動作になるんですか?
線路が集中定数だった場合、ドライバから出力した立上り信号は出力した時点ですでにレシーバに到達していることになる。ドライバからレシーバまでの遅延時間がない(ゼロ)のが集中定数なのじゃ。


ドライバーとレシーバ間の信号線路が十分に長いと分布定数、短いと集中定数として扱うわけですね!?
じゃあ、分布定数と集中定数の境界条件は何ですか?
集中定数と分布定数に関わる文献はたくさんあり様々な見方があるが、厳密な境界条件が決められているわけではないんじゃよ。


えぇ~、そうなんですか~。
・・・
でも線路設計する上で、分布定数として扱わなければならない線路長と
集中定数として扱える線路長は把握しておきたいわ。。
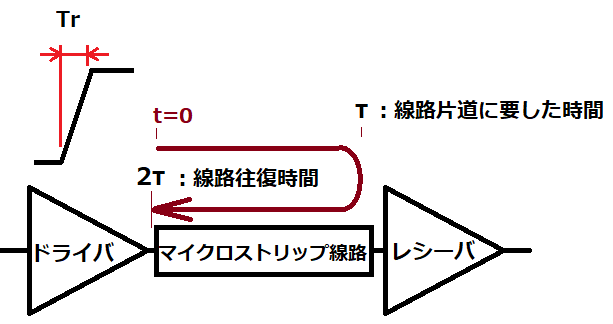 右の図にあるτ(タウとよぶ)は線路片道に要した時間を示している。
右の図にあるτ(タウとよぶ)は線路片道に要した時間を示している。
分布定数と集中定数の境界は、TrまたはTfの状態遷移時間と、ドライバから出力した信号がレシーバ入力端を往復してドライバに戻ってくる時間2τとが等しいときであると言われておる。


 右図のストリップ線路の場合だとどのようになるんですか?
右図のストリップ線路の場合だとどのようになるんですか?
 Tr=1nsとマイクロストリップ線路往復分時間2τが同じになる線路長が境界とするので、
Tr=1nsとマイクロストリップ線路往復分時間2τが同じになる線路長が境界とするので、
線路長Lは、8.21cmになる。
さらに立上り・立下りのリンギングが収束するには5τ~7τ要するといわれておるので、ここでは6τ(3往復分)で算出する。
線路長は、2.73cmとなり、これ以下が集中定数と考える。


 つまり右のような関係ですね。
つまり右のような関係ですね。
昇平博士、参考になります!
今回は集中定数として扱う境界条件を示したわけじゃが、厳密なものではない。
最終的にはドライバ出力端とレシーバ入力端の電圧波形を確認し、特にレシーバ入力端の電圧波形のオーバーシュートとアンダーシュートの有無で集中定数か分布定数かを判断することになる。
オーバーシュートやアンダーシュートがある場合は、線路両端で反射の可能性があるので、インピーダンス(ドライバの出力インピーダンス・線路インピーダンス・レシーバの入力インピーダンス)を確認せねばならんのじゃ。詳細は次回にしよう。


次回は、インピーダンスのお話です。
