
今回は2端子対回路の中に実際のインダクタLを並列接続したときの反射損失と通過損失を求めます。
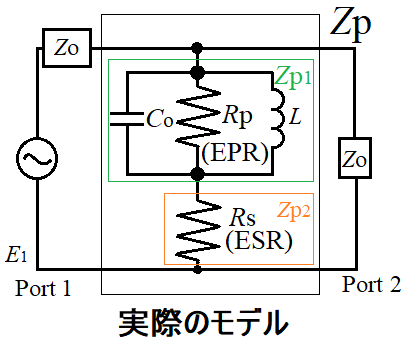
実際のインダクタモデルを並列に接続すると、上の回路図のようなモデルで表すことができる。
最初にZpを求めなければならないので、なみりんよZpを求めてくれないか。


Zpは、Rp、L、Coの3素子から成る並列インピーダンスとRsの直列抵抗の和で表現することができます。上の回路だと、Zp = Zp1 + Zp2で求まります。
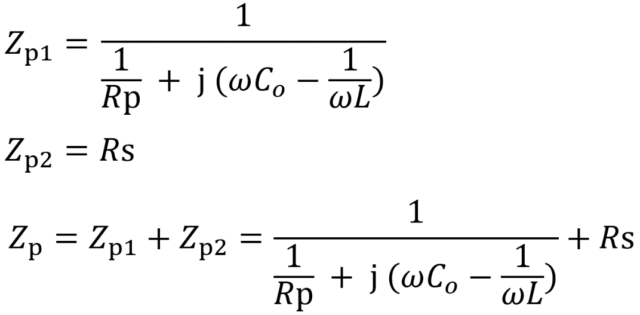
下の式を参考に、複素関数を使ってS11とS21を求めたあとに、反射損失と通過損失を求めるのじゃ。

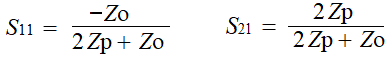

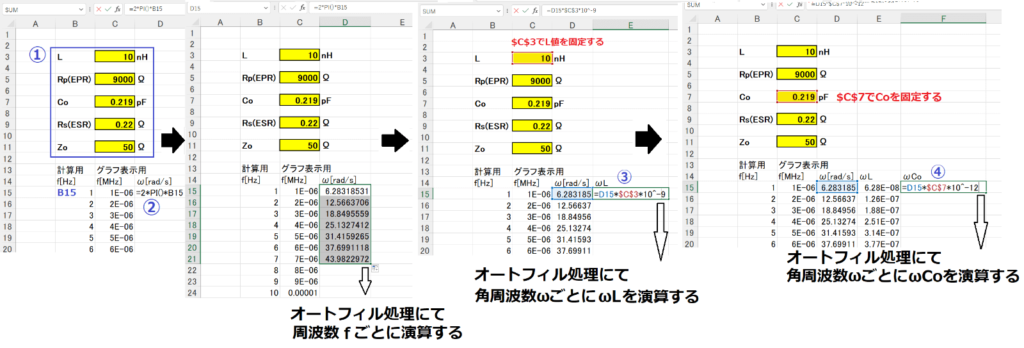
① 最初に初期条件設定として、インダクタLと各パラメータを記述します。
ここではL = 10nH、Rp = 9000Ω、Co=0.219pF、Rs=0.22Ω、Zo=50Ωにします。
② つぎに周波数fを記述し、角速度ω( =2 π f )[rad/s]を求めます。
③ さらに角速度ωとインダクタLとの積でωLを求めます。
④ そのうえに角速度ωと浮遊容量Coとの積でωCoを求めます。
つぎはS11を求めるために複素関数を使って、まずはZpを求めてみるのじゃ。


⑤ Zp = Zp1 + Zp2のうち、Zp1の分母をCOMPLEX関数で記述します。
⑥ Zp1 の分母の実数は1/Rp、虚数はωCo - 1/(ωL)になります。
⑦ Zp1 の分母を複素数化できたので、IMDIVで④の逆数をとります。 これが、Zp1です。
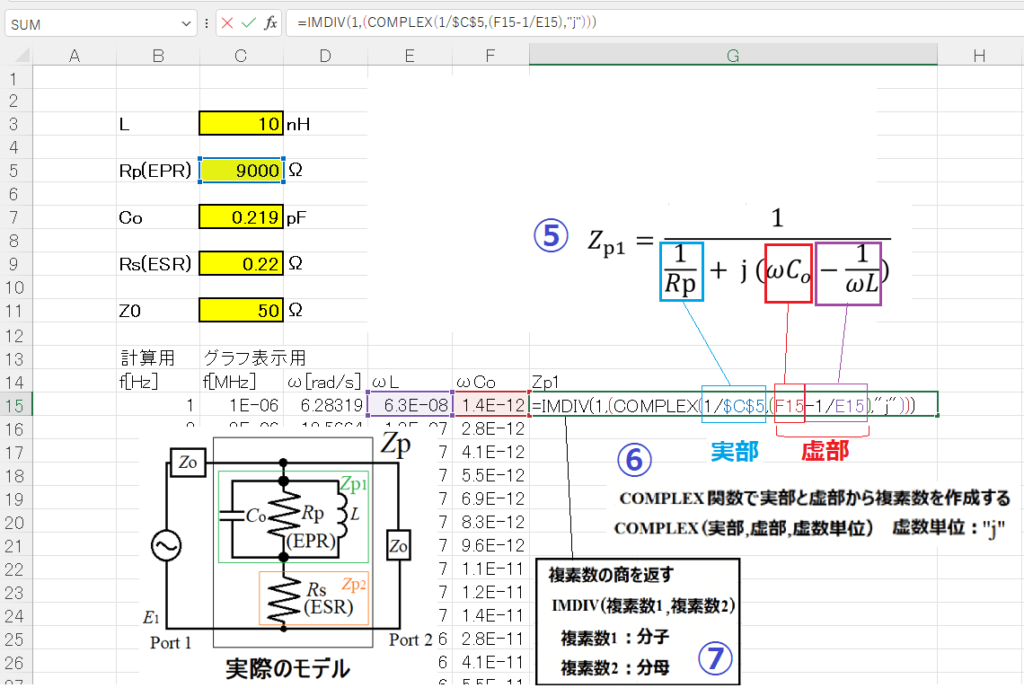

⑧ Zp = Zp1 + Zp2 = Zp1 + Rs からZpを求めます。
⑨ S11を求めます。
⑩ |S11|、反射損失を求めます。
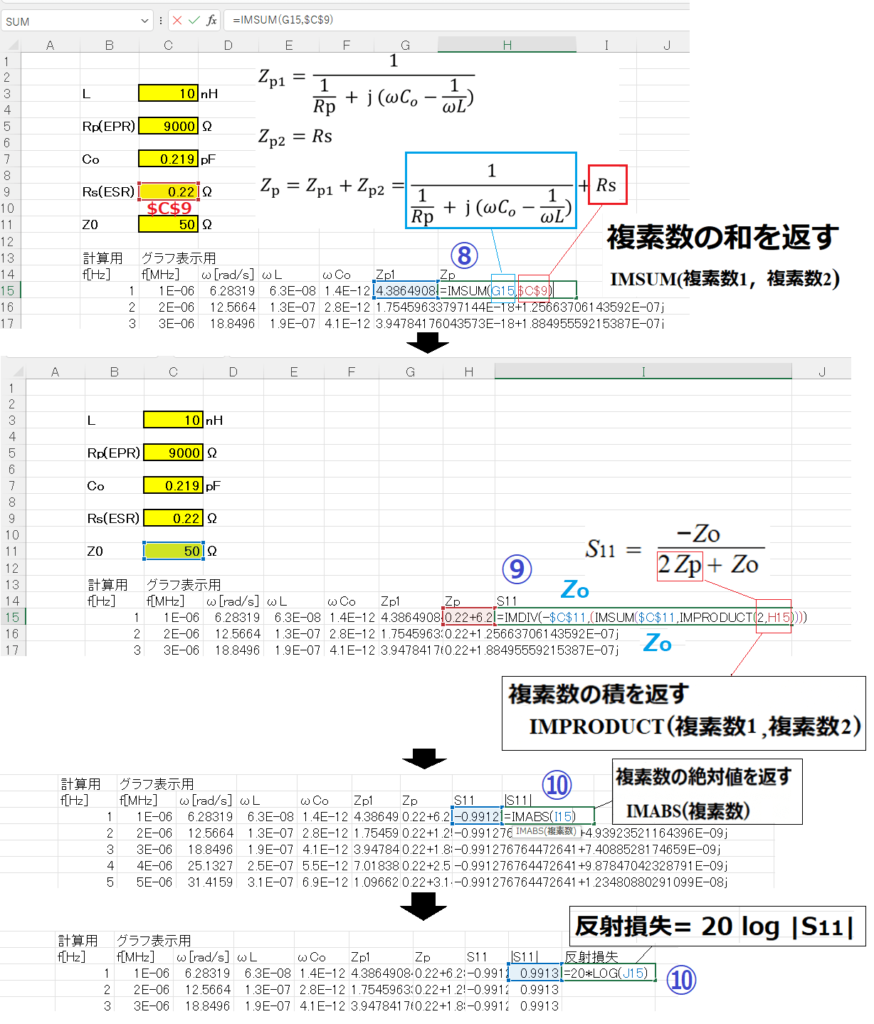
つぎはS21を求めてみるのじゃ。


⑪ S21はZpが既知なので、すぐに求めることができます。
⑫ |S21|、通過損失を求めます。
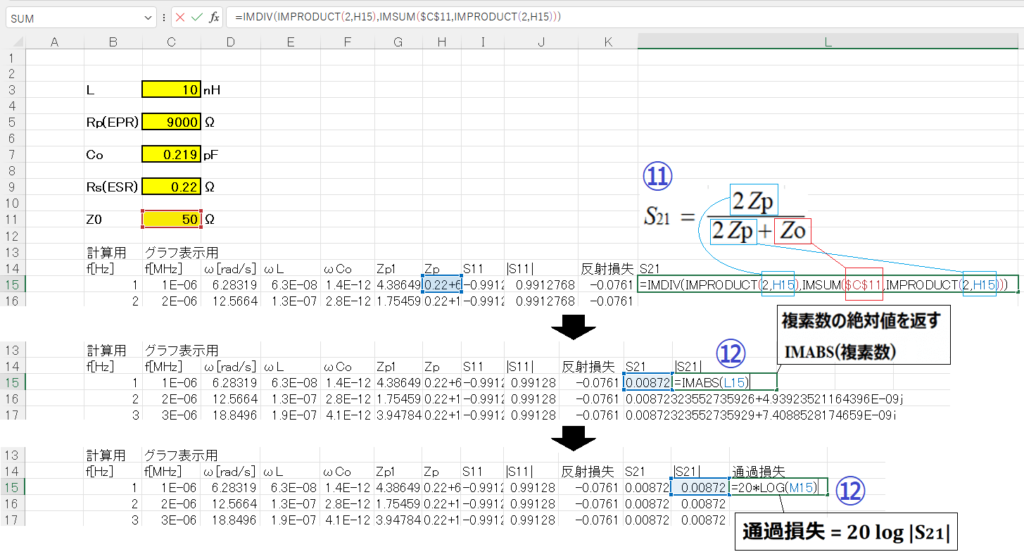
S21から通過損失も求まったようじゃな。
横軸を周波数[MHz]にして、反射損失と通過損失をグラフ化してみるのじゃ。



下のようなグラフになりました。
低周波域では通過損失が大きく、3.4GHzで最小となり、10GHz付近から再び通過損失が大きくなるようです。
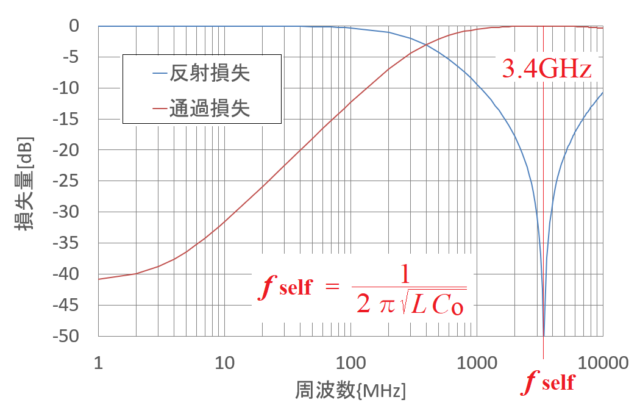
そうじゃな、これはインダクタLに寄生しておる浮遊容量またはストレーキャパシタCoとの間で形成された共振現象(自己共振周波数とよぶ)によるものじゃ。
次はキャパシタンスの並列接続について演習してみよう。

